1.개요
=>여러 비선형 변환 기법의 조합을 통해 높은 수준의 추상화를 시도하는 머신러닝 알고리즘의 집합
=>연속된 층(Layer)에서 점진적으로 의미있는 표현을 배우는 방식
=>기존의 머신러닝 방법은 1~2가지의 데이터 표현을 학습하지는 얕은 학습을 수행하지만 딥 러닝은 수백 개 이상의 층을 이용
=>데이터로부터 표현을 학습하는 수학 모델
=>층을 통과할 때 마다 새로운 데이터 표현을 만들어 가면서 학습

1)작동 원리
=>층에서 입력 데이터가 처리되는 내용은 일련의 숫자로 이루어진 층의 가중치에 저장이 되는데 이는 그 층의 가중치를 parameter로 갖는 함수로 표현
=>이 가중치를 알아낼려면 데이터를 관찰해야 하고 신경망의 출력이 기대하는 것 보다 얼마나 벗어났지를 측정해야 합니다
딥러닝은 기본적으로 지도 학습
지도 학습은 오차를 줄여나가는 작업이므로 오차를 측정하는 함수가 존재해야되는데 이를 손실함수(Loss Function)이라고합니다
=>딥러닝은 이 손실 함수의 값이 감소하는 방향으로 가중치 값을 수정해 나가는 것

=>머신러닝과 딥러닝의 차이는 데이터 변환의 차이.
=>초창기에는 네트워크의 가중치를 랜덤하게 할당하고 랜덤한 변환을 연속적으로 수행하는 방식을 사용했는데 이 방식은 수행을 많이 하게 되면 손실 점수가 높아지게 될 수 있음
2)특징
=>딥 러닝이 확산된 가장 큰 요인은 많은 문제에서 기존의 머신러닝 알고리즘보다 성능이 우수하기 때문
=>특성 공학을 완전히 자동화
기존의 머신러닝 알고리즘들은 대부분 알고리즘이 이해할 수 있도록 데이터를 변환하는 작업을 직접 수행해야 합니다.
딥러닝은 데이터의 좋은 표현을 스스로 만들어 냅니다.
=>딥 러닝이 학습 할 때의 특징
-층을 거치면서 점진적으로 더 복잡한 표현을 만들어 냄
- 점진적인 표현을 만드는 작업을 순차적으로 하는 것이 아니고 공동으로 학습
3)최근 경향
=>2010년대 후반까지는 Kaggle에서 GBM 과 Deep Learning 을 사용한 모델이 우승을 차지 햇는데 GBM은 구조적인 데이터에 사용하고 Deep Learning 은 이미지 분류와 지각에 관한 문제에 사용
GBM 모델 중에서도 XGBoost 가 주로 이용되었습니다
=>패턴 인식 분야에서는 최근에는 거의 무조건 Deep Learning 을 사용 (시계열 분석)
=>딥 러닝을 많이 사용하게 된 이유 중의 하나는 하드웨어의 발전이고 다른 하나는 데이터의 증가입니다
4)장점
=>성능이 우수
=>특성 공학이 자동
=>구조화 되지 않은 데이터 학습 능력이 뛰어남
5)제한
=>학습 데이터가 많아야 함
=>네트워크가 만들어 낸 특성을 해석하기가 어려움
=>컴퓨팅 자원이 많이 필요
=>데이터의 크기가 기가 바이트를 넘지 않는다면 딥러닝과 머신러닝은 별 차이가 없다고 합니다
6)딥러닝 패키지
=>Torch:C로 구현된 라이브러리로 facebook에서 Torch로 만들 PyTorch를 내놓으면서 유명해짐
과학 기술 연구용으로 많이 사용됨. 자유도가 높
=>Theano:numpy 배열과 관련성이 높은 패키지로 계산을 많이 하는 연구에 이용
구글의 오픈 소스인 TensorFlow 가 Theano 에서 영감을 얻는 라이브러리
Production 구현이 강력 - PC, Android, Web 용 라이브러리를 제공
제품을 만들 때는 TensorFlow를 많이 사용함
=>CuDNN: CUDA Deep Neural Network의 약자로 GPU 구현을 위한 라이브러리를 제공
2.인공신경망
1)개요
=>지능적인 기계를 만드는 법에 대한 영감을 얻으려면 뇌 구조를 살펴보는 것이 합리적이라고 판단했는데 이 것이 인공 신경망(ANN-Artificial Neural Network)이라고 붙이게 된
=>인공 신경망은 뇌에 있는 생물학적 뉴런의 네트워크에서 영감을 받은 머신러닝 모델이지만 새를 보고 비행기에 대한 영감을 얻었다고 해서 비행기 날개를 새처럼 펄럭 거릴 필요는 없는데 인공 신경망도 생물학적 뉴런에서 점점 멀어지고 있음
=>일부에서는 neuron 이라는 표현 대신에 unit 이라고 지칭
=>1943년에 워런 매컬러의 논문에서 처음 소개
2)뉴런을 이용한 논리 연산
=> 가장 처음 만든 모델은 하나 이상의 이진 입력과 이진 출력하는 가짐
=> 이 모델을 가지고 not , or ,and 연산을 수행
3)Perceptron
=>입력과 출력이 이진이 아닌 숫자이고, 각각의 입력 연결은 가중치 와 연관되어 있음
=>입력의 가중치 합을 계산한 뒤 계산된 합에 함수(계단 함수 -step function)을 적용해서 결과를 출력
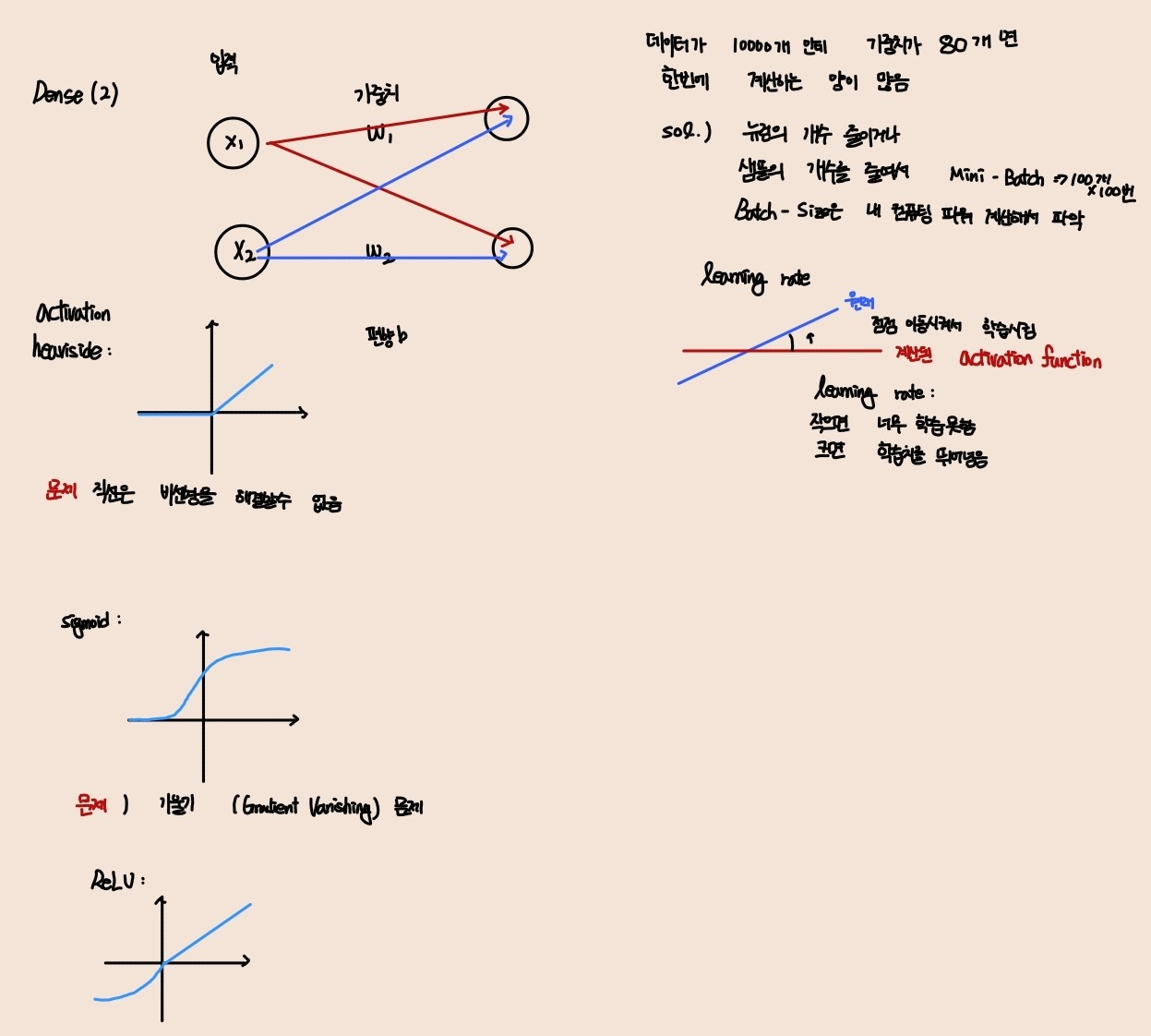
가장 많이 사용되는 계단 함수가 heavisidde 와 sign function
heaviside 는 가중치의 합이 0보다 작으면 0 0보다 크거나 같으면 1을 리턴하는 함수
sign function은 가중치의 합이 0 보다 작을 때 -1 0보다 클 때 1을 리턴하는 함수
=>이러한 Perceptron이 여러개 모여서 하나의 layer 를 구성하게 되고 이전 층의 모든 뉴론과 연결이 되면 이를 Fully Connected Layer(완전 연결 층) 또는 Dense layer(밀집층)
=> 입력은 입력 뉴런이라고 하는 특별한 뉴런에 주입이 되는데 이러한 입력 뉴런으로 구성된 레이어를 Input layer 라고 부르고 이 레이어가 다른 레이어와 다른 점은 편향 특성이 더해지는데 (x0 = 1) 이 편향 특성은 항상 1을 출력하는 특별한 종류의 뉴런이라고 해서 편향 뉴런(Bias Neuron)이라고 표현
=> Perceptron은 선형 분류 모형의 형태를 갖게 됩니다.
논리 연산 중 XOR 문제를 해결하지 못함
4)MLP
=>Perceptron 이 지니고 한계점을 극복하기 위해서 여러개의 layer 를 쌓아 올린 MLP (Multi Layer Perceptron)이 등장
=>Perceptron은 기본적으로 input과 output layer 로만 구성되지만 MLP는 이 중간에 Hidden Layer 를 추가한 형태
Hidden layer 는 여러개의 Perceptron이 모여있는 구조
이 때 Hidden Layer 를 여러 개 쌓으면 깊어지기 때문에 이를 Deep learning 이라고 부름
=>Input 에서 Weight 을 계산하고 Hidden layer를 거쳐서 Output를 만들어내는데 이과정을 Feed Forward 라고 합니다.
5)Activation Function
=>어떤 신호를 받아서 이를 적절히 처리해서 출력해주는 함수
=>Input과 Weight 를 받아서 연산을 수행해주는 함수
=>신경망은 비선형 Activation Function 을 선호
=>Sign Function , Heaviside step, Sigmoid (로그 함수- 1/(1+e의 -x승))
Sigmoid 함수는 입력 값이 0 이하면 0.5 이하의 값을 출력하고 0이상이면 0.5 이상의 값을 출력하는데 입력 값에 대해서 0과 1사이의 값으로 Scaling해주는 개념의 함수
Sign Function과 Heaviside 는 선형이고 Sigmoid 는 비선형
대부분의 경우 비선형이 선형보다 우수한 성능을 발휘하기 때문에 신경망은 비선형을 선호
Sigmoid 함수는 복잡한 문제를 해결할수 있는데 Back Propagation 과정 중 Gradient Vanishing(소멸) 현상이 발생 가능
모델이 깊어질수록 이러한 현상이 자주 발생
- softmax 함수
Sigmoid 을 일반화 시킨 함수로 다중 클래스 분류에 가장 적합

- ReLU (Rectified Linear Unit)
전체 입력이 0보다 크면 출력은 순입력(가중치를 곱하고 편향을 더한 값)과 같고 전체 입력이 0보다 작거나 같으면 0을 출력
y = max(0,가중치*입력 + 편향)
ReLU는 입력이 양수이고 기울기가 0이어도 일정한 기울기를 가지게 됨

양수만 보면 선형이지만 0이나 0보다 작을 때 0의 값을 갖도록 해서 비선형을 만들어 냄
음수일 때도 기울기를 가지도록 만들어진 함수가 잇는데 이 함수는 PReLU
나중에 딥러닝할때 함수 이름을 직접 입력해야함
- Hyperbolic Tangent : tanh
출력이 0인 지점에서 기울기를 가짐


6)Learning Rate(학습률)
=> 경사 하강법에서 가중치를 업데이트할 때 간격
=>숫자가 커지면 최적의 지점을 찾지 할 수 있고 너무 작은 값을 선택하면 학습속도가 느려질 수 있음
=>신경망에서는 0.01 아래 의 값을 사용하는 것을 권장
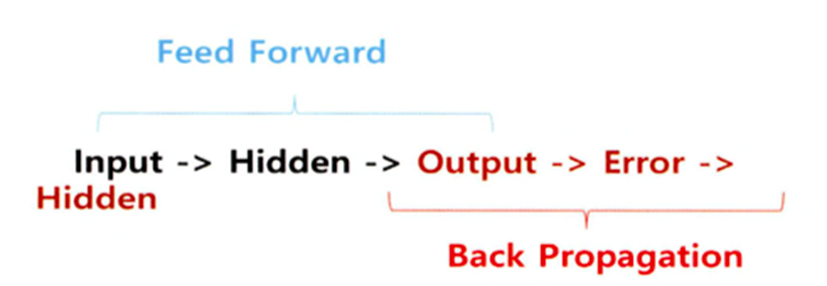
7)Back Propagation(역전파)
=>Input 에서 Output 까지 계산을 수행하고 그 결과를 가지고 실제 답과의 오차를 구해서 오차가 작아지는 형태로 가중치를 조정할 때 뒤에 있는 가중치를 먼저 업데이ㅡ한다고 해서 역전파 알고리즘이라고 부름
=>한번 Feed Forward 로 작업을 수행하고 Back Propagation을 수행하면 1번의 epoch라고 함

=>알고리즘을 수행할 때 모든 데이터를 가지고 한꺼번에 하지는 않고 일반적으로 mini batch라고 부르는 작은 단위로 실행
3.Tensorflow
1)개요
=>구글이 만든 딥러닝의 초점에 맞춘 라이브러리
=>GPU를 지원
=>분산 컴퓨팅을 지원 : 여러 대의 컴퓨터에서 동시에 학습 가능하고 예측도 가능 ex.)알파고는 1000대로 만듬
=>플랫폼에 중립적인 포맷으로 내보낼 수 있음
리눅스를 사용하는 파이썬 환경에서 Tensorflow 모델을 훈련시키고 이 모델을 안드로이드에서 실행할 수 있음
2)API
=>거의 모든 운영체제 지원하고 TensorFlow Lite을 이용하면 안드로이드와 iOS 와 같은 모바일 운영체제에서도 실행되고 Python API를 많이 이용하지만 C++,Java ,Go, Swift API도 제공됨
=>Tensorflow Hub 에서 사전에 훈련된 신경망을 쉽게 다운로드 받아서 사용할 수 있음
https://www.tensorflow.org/resources
모델 및 데이터 세트 | TensorFlow
저장소와 기타 리소스를 탐색하여 TensorFlow 커뮤니티에서 만든 모델 및 데이터 세트를 찾아보세요.
www.tensorflow.org
3)연산
=>가장 저 수준의 연산은 C++코드로 만들어져 있음
=>연산들이 여러 종류의 커널에서 수행:CPU,GPU,TPU 등
TPU는 Deep Learning 연산을 위해 특별하게 설계된 ASIC Chip
4)설치
=>pip install tensorflow
4.Tensorflow사용
1)Tensor 생성
=>numpy의 ndarray와 유사한 방식으로 생성
=>immutable data(변경이 불가능한 데이터)
tf.constant(42)
t = tf.constant([[1,2,3],[4,5,6]])
print(t)
print(t[:,1:]) #1번째 열부터 모든 열
print(t[:,1,tf.newaxis]) # 데이터를 분할한 후 새로운 축으로 만들어서 출력
#이거 활용하면 1차원 배열이 2차원 배열이 됩니다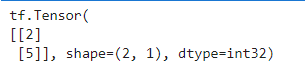
2)연산
=>numpy의 ndarray와 거의 동일한 방식으로 연산을 수행하고 함수나 메서드의 이름도 거의 일치
print(t+10) #broadcast 연산
print(tf.square(t))
tf.transpose(t)@ t
=>tensorflow 나 numpy 에서 배열을 가지고 산술 연산을 하는 경우 실제로는 함수가 호출됩니다
python에서는 __이름__ 형태로 메서드를 만드는 경우가 있는데 이러한 함수들은 Magic Function이락 부르는데 사용할 때 메서드 이름을 호출하는 것이 아니라 다른 연산자를 이용합니다.
이렇게 연산자의 기능을 변경하는 것을 연산자 오버로딩이라고 합니다.
이것은 객체 지향에서만 가능합니다.
+는 숫자 2개를 더하는 기능을 가지고 있는데 tensorflow 나 numpy에서는 __add__ 를 정의해서 이 메서드를 호출하도록 합니다.
파이썬하는 사람들은 magic function이라고 부름. => 연산자 오버라이딩
np.array([1,2])+2 => np.array([1,2]).__add__(2) =>np.array([1,2]).__add__(np.array([2,2]))
=>이름이 다른 함수도 있음
np.mean => tf.reduce_mean

=>tf.float32는 제한된 정밀도를 갖기 때문에 연산을 할 때마다 결과가 달라질 수 있음
=>동일한 기능을 하는 함수나 클래스를 Keras 가 별도로 소유하고 있는 경우도 있음
=>Keras는 Tensorflow의 저수준 API (Core 에 가까운 쪽) =>C++ 에 가까운 쪽
3)Tensor의 numpt의 ndarray
=>2개의 데이터 타입은 호환이 되서 서로 변경이 가능
=>Tensor를 ndarray 로 변환하고자 하는 경우는 numpy() 메서드를 호출하면 되고, numpy의 array 함수에 Tensor를 대입해도 됩니다.
ndarray 를 가지고 Tensor를 만들고자 할 때는 constant 나 variable 같은 함수에 대입하면됩니다.
4)타입 변환
=>Data Type이 성능을 크게 감소시킬 수 있음
=>Tensorflow 는 타입을 절대로 자동변환하지 않습니다
데이터 타입이 다르면 연산이 수행되지 않음
=>타입이 다른데 연산을 수행하고자 하는 경우에는 tf.cast 함수를 이용해서 자료형을 변경해야 합니다.
=>Tensorflow가 형 변환을 자동으로 하지 않는 이유는 사용자가 알지 못하는 작업은 수행을 하면 안된다는 원칙 때문
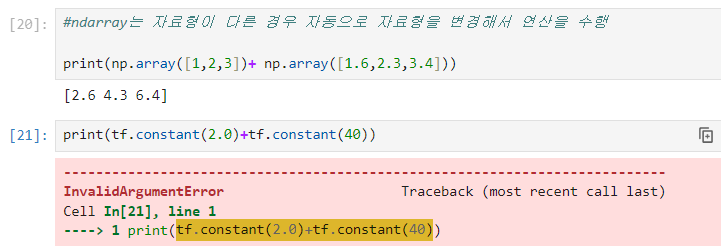
자료형이 달라서 에러가 발생 =>numpy은 문제가 없지만 tensor는 안됨
이런 경우에 형변환을 해야함
t1 =tf.constant(40)
#형 변환 후 연산 수행
print(tf.constant(2.0)+tf.cast(t1,tf.float32))★ InvalidArgumentError: 자료형이 달라서 발생하는 문제
5)변수
=>일반적인 데이터는 직접 변경을 하지 않기 때문에 constant 로 생성해서 사용하면 되는데 역전파 알고리즘을 수행하게 되면 가중치가 업데이트된다고 했는데 가중치는 수정되어야 하기 때문에 constant로 생성되면 안됨
=>수정되어야 하는 데이터는 tf.Variable 을 이용해서 생성
데이터를 수정하고자 하는 경우는 assign 함수를 이용
assign_add 나 assign _sub를 이용해서 일정한 값을 더하거나 빼서 수정할 수 있음
=>배열의 일부분을 수정할 때는 assign 함수나 scatter_update() 나 scatter_nd_update ()를 이용
#변수 생성
v = tf.Variable([[1, 2, 3], [4, 5, 6]])
print(v)
print(id(v))
#이 경우는 데이터를 수정한 것이 아니고
#기존 데이터를 복제해서 연산을 수행한 후 그 결과를 가리키도록 한 것
#참조하는 위치가 변경됨
v = v * 2
print(v)
print(id(v))
#내부 데이터 수정
v = tf.Variable([[1, 2, 3], [4, 5, 6]])
print(v)
print(id(v))
#이 경우는 id 변경없이 데이터를 수정
v.assign(2 * v)
print(v)
print(id(v))
6)Data 구조
=>종류
- SparseTensor: 0이 많은 Tensor를 효율적으로 나타내는데 tf.sparse 패키지에서 이 Tensor에 대한 연산을 제공
- TensorArray: Tensor의 list
- RaggedTensor: list 의 list
- stringtensor: 문자열 텐서인데 실제로는 바이트 문자열로 저장됨
- set
- queue
7)Tensorflow 함수
=>일반 함수는 python 의 연산 방식에 따라 동작하지만 Tensorflow 함수를 만들게 되면 Tensorflow 프레임워크가 자신의 연산 방식으로 변경해서 수행을 하기 때문에 속도가 빨라질 가능성이 높음
=>Tensorflow 함수를 만드는 방법은 함수를 정의한 후 tf.function 이라는 decorator를 추가해도 되고 tf.function 함수에 함수를 대입해서 리턴받아도 됩니다.
=>함수를 변경하는 과정에서 Tensorflow 함수로 변경이 불가능하면 일반 함수로 변환을 합니다.
8)난수 생성
=>tf.random 모듈을 이용해서 난수를 생성
5.뉴런 생성
=>뉴런을 추상화하면 Perceptron 이라고 합니다.
1)기본 구조
입력 -> 뉴런 -> 출력
=>이런 여러 개의 뉴런이 모이면 Layer 라고 하며 이런 Layer의 집합이 신경망
2)뉴런의 구성
=>입력, 가중치, 활성화 함수, 출력으로 구성
=>입력 과 가중치 와 출력은 일반적으로 정수 나 실수
=>활성화 함수는 누런의 출력 값을 정하는 함수
=>간단한 형태의 뉴런은 입력에 가중치를 곱한 뒤 활성화 함수를 취하면 출력을 얻어 낼 수 있음
=>뉴런은 가중치를 처음에는 랜덤하게 초기화를 해서 시작하고 학습 과정에서 점차 일정한 값으로 수렴
학습 할 때 변하는 것은 가중치
=>활성화 함수는 시그모이드나 ReLU 를 주로 이용
최근에는 주로 ReLU를 주로 이용
=>뉴런을 직접 생성
#시그모이드 함수
import math
def sigmoid(x):
return 1 / (1 + math.exp(-x))
#입력
x = 1
#출력
y = 0
#한번 학습
w = tf.random.normal([1], 0, 1) #가중치
output = sigmoid(x * w)
print(output)
=>경사하강법을 이용한 뉴런의 학습
#경사하강법에서는 학습률을 설정해야 합니다.
#학습률을 0.01 로 설정해서 경사하강법을 수행
#학습 횟수 - epoch
for i in range(1000):
#출력을 생성
output = sigmoid(x * w)
#출력 오차를 계산
error = y - output
#가중치 업데이트
w = w + x * 0.1 * error
#횟수 와 오차 그리고 출력값을 확인
if i % 100 == 0:
print(i, error, output)
#학습을 할 수 록 결과인 0에 가까워짐
=>입력이 0일 때 1을 얻는 뉴런 - 결과가 이상
#입력
x = 0
#출력
y = 1
#학습률을 0.01 로 설정해서 경사하강법을 수행
#학습 횟수 - epoch
for i in range(1000):
#출력을 생성
output = sigmoid(x * w)
#출력 오차를 계산
error = y - output
#가중치 업데이트
w = w + x * 0.1 * error
#횟수 와 오차 그리고 출력값을 확인
if i % 100 == 0:
print(i, error, output)
#입력 데이터가 0 이고 가중치를 업데이트하는 식이 w + x * 0.1 * error 라서 x 가 0이 되면 가중치를 업데이트 할 수 없습니다.
#단순하게 시그모이드 함수를 적용하면 이 경우 최적점에 도달할 수 없고 계속 0.5 만 출력
#입력 데이터 0에서 기울기가 없어지는 현상 - 기울기 소실 문제(Gradient Vanishing)
#이 경우에는 시그모이드 함수 대신에 0에서 기울기를 갖는 ReLU를 사용하거나 시그모이드 함수에 데이터를 대입할 때 편향을 추가해서 해결합니다.
#입력
x = 0
#출력
y = 1
#가중치
w = tf.random.normal([1], 0, 1)
#편향 생성
b = tf.random.normal([1], 0, 1)
#학습률을 0.01 로 설정해서 경사하강법을 수행
#학습 횟수 - epoch
for i in range(1000):
#출력을 생성
output = sigmoid(x * w + 1 * b)
#출력 오차를 계산
error = y - output
#가중치 업데이트
w = w + x * 0.1 * error
#편향 업데이트
b = b + 1 * 0.1 * error
#횟수 와 오차 그리고 출력값을 확인
if i % 100 == 0:
print(i, error, output)
#입력
x = 0
#출력
y = 1
#가중치
w = tf.random.normal([1], 0, 1)
#편향 생성
b = tf.random.normal([1], 0, 1)
#학습률을 0.01 로 설정해서 경사하강법을 수행
#학습 횟수 - epoch
for i in range(1000):
#출력을 생성
output = sigmoid(x * w + 1 * b)
#출력 오차를 계산
error = y - output
#가중치 업데이트
w = w + x * 0.1 * error
#편향 업데이트
b = b + 1 * 0.1 * error
#횟수 와 오차 그리고 출력값을 확인
if i % 100 == 0:
print(i, error, output)
3)AND을 구현
=>AND을 연산
0 0 -> 0
0 1 -> 0
1 0 -> 0
1 1 -> 1
입력 피처는 2개이고 출력은 1개
가중치는 2개가 되어야 합니다.
가중치는 입력 피처마다 설정이 됩니다.
X = np.array([[0,0],[0,1],[1,0],[1,1]])
y = np.array([[0],[0],[0],[1]])
w = tf.random.normal([2],0,1) #입력 feature 가 2개이므로 가중치가 2개
b = tf.random.normal([1],0,1) #편향
b_x = 1
import math
def sigmoid(x):
return 1 / (1 + math.exp(-x))
for i in range(2000):
error_sum = 0
for j in range(4):
#출력
output = sigmoid(np.sum(X[j]*w)+b_x*b)
#오차
error = y[j][0] - output
#가중치 업데이트 - 학습률은 0.1
w = w + X[j] * 0.1 * error
#편향 업데이트
b = b + b_x * 0.1 * error
error_sum += error
if i % 200 == 199:
print(i, error_sum)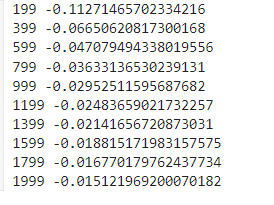
#예측한 값 확인
for i in range(4):
print('X:',X[i],"y:",y[i],sigmoid(np.sum(X[i])+b))
[ 0 0] 일때 가장 정확하게 예측했습니다.
4)XOR 구현
X = np.array([[0,0],[0,1],[1,0],[1,1]]) #같으면 0 다르면 1
y = np.array([[0],[1],[1],[0]])
w = tf.random.normal([2],0,1) #입력 feature 가 2개이므로 가중치가 2개
b = tf.random.normal([1],0,1) #편향
b_x = 1
import math
def sigmoid(x):
return 1 / (1 + math.exp(-x))
for i in range(2000):
error_sum = 0
for j in range(4):
#출력
output = sigmoid(np.sum(X[j]*w)+b_x*b)
#오차
error = y[j][0] - output
#가중치 업데이트 - 학습률은 0.1
w = w + X[j] * 0.1 * error
#편향 업데이트
b = b + b_x * 0.1 * error
error_sum += error
if i % 200 == 199:
print(i, error_sum)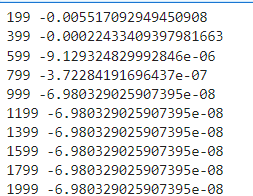
#예측한 값 확인
for i in range(4):
print('X:',X[i],"y:",y[i],sigmoid(np.sum(X[i])+b))
앞에 and와 다르게 4개의 출력결과가 거의 비슷
가중치를 출력해보면 첫번째 가중치가 두번째 가중치보다 2배 정도 더 큽니다. 첫번째 데이터의 영향력이 커져서 첫번째 데이터에 의해서 값이 결정될 가능성이 높습니다.
즉 XOR 문제는 하나의 선으로는 해결할 수 없는 문제
이런 경우에는 여러 개의 선을 그어서 해결 - Layer를 여러개 만들어주어야 합니다.
=>XOR 문제 해결
X = np.array([[0,0],[0,1],[1,0],[1,1]]) #같으면 0 다르면 1
y = np.array([[0],[1],[1],[0]])
w = tf.random.normal([2],0,1) #입력 feature 가 2개이므로 가중치가 2개
b = tf.random.normal([1],0,1) #편향
b_x = 1
#2개의 완전 연결층을 가진 모델 생성
#units 는 뉴런의 개수이고 activation은 출력을 계산해주는 함수
#input_shape 은 맨 처음 입력 층에서의 feature 모양 생성
model = tf.keras.Sequential([
tf.keras.layers.Dense(units=2,activation='sigmoid',input_shape=(2,))
])
model.compile(optimizer = tf.keras.optimizers.SGD(learning_rate=0.1),loss='mse')
model.summary()
#훈련
#batch_size 는 한 번에 연산되는 데이터의 크기(Mini Batch)
history = model.fit(X,y,epochs=10000,batch_size=1)
=>이게 위의 내용과 같음
크게 변동이 없는걸 보고 Layer 하나더 추가
X = np.array([[0,0],[0,1],[1,0],[1,1]]) #같으면 0 다르면 1
y = np.array([[0],[1],[1],[0]])
w = tf.random.normal([2],0,1) #입력 feature 가 2개이므로 가중치가 2개
b = tf.random.normal([1],0,1) #편향
b_x = 1
#2개의 완전 연결층을 가진 모델 생성
#units 는 뉴런의 개수이고 activation은 출력을 계산해주는 함수
#input_shape 은 맨 처음 입력 층에서의 feature 모양 생성
model = tf.keras.Sequential([
tf.keras.layers.Dense(units=2,activation='sigmoid',input_shape=(2,)),
tf.keras.layers.Dense(units=1,activation='sigmoid')
])
model.compile(optimizer = tf.keras.optimizers.SGD(learning_rate=0.1),loss='mse')
model.summary()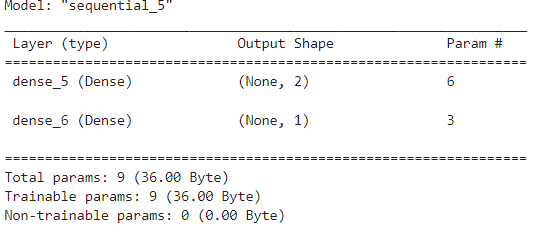
다시 재학습하고 나서 loss 확인
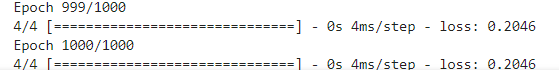
result = model.predict(X)
print(result)이걸 활용해서 result 값을 최대한 올려보면됨. 하이퍼파라미터 조정이나 epochs 를 키우는 방향으로 진행하면됨
#측정치 변환량(손실의 변화량)
import matplotlib.pyplot as plt
plt.plot(history.history['loss'])
6.Tensorflow Data API
1)개요
=>Machine learning 을 하는 경우 대규모 데이터 세트를 사용해야 하는 경우가 있는데 이 경우 Data를 Load 하고 Preprocessing 을 수행하는 작업은 번거로운 작업이며 데이터를 어떻게 사용할 것인가 하는 것도 어려운 작업(Multi Threading, Queue,Batch,Prefetch등) 중 하나
=>Tensorflow Data API는 dataset 객체를 만들고 Data 를 읽어올 위치와 변환 방법을 지정하면 이러한 작업을 자동으로 처리
=>Data API는 텍스트 파일(csv, tsv등),고정 길이를 가진 이진 파일, Tensorflow 의 TFRecord 포맷을 사용하는 이진 파일에서 데이터를 읽을 수 있습니다.
관계형 데이터 베이스나 Google Big Query 와 같은 NoSQL 데이터베이스에서 데이터를 읽어올 수 있습니다.
=>Tensorflow 에서는 One-Hot Encoding이나 BoW Encoding, embedding 등의 작업을 수행해주는 다양한 Preprocessing층도 제공
2)프로젝트
=>TF 변환
=>TF DataSet(TFDS)
-dataset 을 다운로드 할 수 있는 편리한 함수를 제공
-이미지 넷과 같은 대용량 dataset 이 포함되어 있음
=>tensorflow datasets 가면 데이터셋을 불러올 수 있음
tfds.load 함수를 호출하면 Data를 다운로드 하고 dataset 의 디셔너리로 Data 를 리턴
=>mnist 데이터 가져오기
import tensorflow_datasets as tfds
datasets = tfds.load(name='mnist')
print(type(datasets))

'Study > Deep learning' 카테고리의 다른 글
| Deep learning(6) - 자연어처리 (1) | 2024.03.25 |
|---|---|
| Deep Learning(5)-RNN (0) | 2024.03.22 |
| Deep learning(4) - CNN (0) | 2024.03.21 |
| Deep Learning(3) - Optimizer 와 activation함수 알아보기 (0) | 2024.03.20 |
| DeepLearning(2)-딥러닝 기초 (0) | 2024.03.19 |



