1.다변량 검색
1)상관계수
=>상관 계수를 구하기 전에 산점도 등을 통해서 상관 계수를 구하는 것이 의미가 있는지 확인
- matplotlib.pyplot 의 scatter 함수 이용
-panda의 plot 함수를 호출하고 kind
-seaborn의 fairplot 함수를 이용할 수 있는데 이 함수는 DataFrame을 이용하면 모든 숫자의 컬럼 사용ㅇ 가능
-seaborn에서는 regplot(산점도와 회귀 jointplot 같은 두개의 컬럼만으로 산점도와 히스토그램을 같이 그릴 수 있습니다.
=>상관계수 조류
-피어슨 상관 계수
-스피어만 상관 계수
-켄달 상관 계수
=>피어슨 상관 계수
-일반적인 상관 계수
-특잇값에 영향을 많이 받음
-선형 관계만 파악이 가능:비선형 관계는 제대로 파악을 하지 못할 수 있습니다
-pandas 의 DataFrame 에는 corr이라는 함수를 이용해서 상관계수를 구할 수 있음
-pandas의 이전 버전에서는 DataFrame에 숫자가 아닌 컬럼이 존재하면 제외하고 상관계수를 리턴했는데 최신버전에서는 이 경우에 에러 발생
-scipy의 stats 패키지에서도 pearsonr 이라는 상관 계수를 구해주는 함수를 제공하는데 이 함수는 피어슨 상관 계수와 유의 확률 (p-value)을 리턴
=>데이터 의 상관관계를 상관계수로만 판단하면 안됨
-앤스콤 데이터
상관 계수로 분포의 형상을 추측할 때 개별 자료가 상관 계수에 미치는 영향력이 서로 다름
피어슨 상관 계수는 이상치나 극단치에 영향을 크게 받는 경우가 발생하고 비선형 관계를 반영하지 못함
앤스콤 데이터는 4 그룹의 데이터를 가지고 있는데 각 데이터 그룹의 상관 계수가 0.816 으로 동일
첫번째 그룹은 일반적인 데이터 그룹이고, 두번째 그룹은 완전한 비선형 상관 관계를 가지고 있는 데이터셋 인데
피어슨 상관계수가 비선형 관계는 정확히 반영하지 못하기 때문에 0.816의 값을 가지게 되고, 세번째 그룹과 네번째 그룹은 이상한 데이터 1개가 영향력을 크게 미쳐서 상관 계수가 0.816 이 되어버립니다.
import statsmodels.api as sm
data= sm.datasets.get_rdataset('anscombe')
df=data.data
print(df)
#피어슨 상관계수 확인
print(df.corr())
plt.subplot(221)
sns.regplot(x='x1',y='y1',data=df)
plt.subplot(222)
sns.regplot(x='x2',y='y2',data=df)
plt.subplot(223)
sns.regplot(x='x3',y='y3',data=df)
plt.subplot(224)
sns.regplot(x='x4',y='y4',data=df)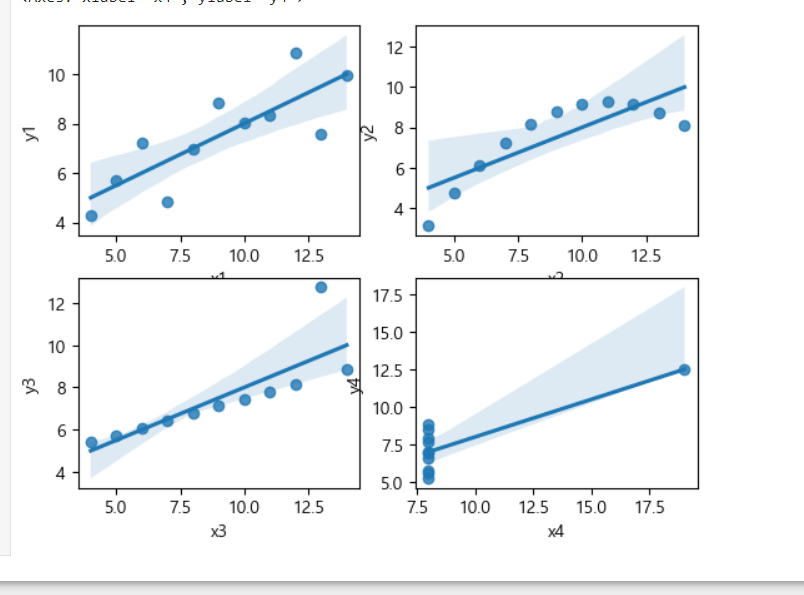
=>상관 계수는 동일하지만 분포는 아예다르다는 것을 볼 수 있음
=>스피어만 상관 계수( spearman)
-순위를 가지고 상관 계수를 만들어내는 방식
-값을 가지고 하지 않기 때문에 비선형 관계도 파악할 수 있습니다
-순위를 기반으로 하기 떄문에 연속형 데이터가 아니더라도 적용이 가능
-pandas에서는 corr 함수의 method 라는 옵션에 spearman을 설정하면 되고 scipy.stats.spearman(데이터 1개,데이터 1개, axis=0)
=>스피어만 상관 계수 확인
s1=pd.Series([1,3,5,7,9])
s2=pd.Series([1,9,25,49,81])
sns.regplot(x=s1,y=s2,data=df)
#피어슨 상관계수
print("피어슨 상관계수:",s1.corr(s2))
#스피어만 상관계수 = 비선형의 경우 조금 더 정확하게 반영
print("스피어만 상관계수:",s1.corr(s2,method='spearman'))
=>kendal의 상관계수
-스피어만 상관 계수와 비슷한데 이번에는 순위를 기반으로 하는 것이 아니고 값의 증감만 확인해서 상관계수를 생성
-pandas에서는 method=kendall을 설정하면 되고 scipy.stats.kendalltau을 호출하면 됩니다
#피어슨 보다는 비선형에서 조금 더 나은 결과를 만들어내고 이상치에 대해서도 robust
print("1의 켄달 상관 계수:",sp.stats.kendalltau(df['x1'],df['y1']))
print("2의 켄달 상관 계수:",sp.stats.kendalltau(df['x2'],df['y2']))
print("3의 켄달 상관 계수:",sp.stats.kendalltau(df['x3'],df['y3']))
print("4의 켄달 상관 계수:",sp.stats.kendalltau(df['x4'],df['y4']))
2)수치형 데이터와 수치형 데이터의 분포 시각화
=>산점도
-데이터의 개수가 상대적으로 적을 때는 무난하지만 수십,수백만의 레코드를 나타내기에는 점들이 너무 밀집되서 알아보기 어려움
sns.jointplot(x='total_bill',y='tip',data=tips,kind='scatter')
=>육각형 구간 차트
-데이터를 점으로 표시하는 대신 기록값들을 육각형 모양의 구간들로 나누고 각 구간에 포함된 기록닶의 개수에 따라 색상을 표시
-색상의 모양이 구름의 형태로 표현됨
-seaborn 패키지의 plot 계열의 함수에 kind를 hex로 설정하면 데이터의 분포를 점 대신 육각형으로 표시
sns.jointplot(x='total_bill',y='tip',data=tips,kind='hex')
=>등고선 차트
-두 변수로 이루어진 지형에서의 등고선
-matplotlib.pyplot 에서는 contoutf 함수를 이용하고 seaborn에서는 kdeplot 을 이용할 수 있습니다.
-데이터가 많을 때 사용
-데이터가 많으면 그리는데 시간이 오래 걸림
3)범주형 데이터와 범주형 데이터의 시각화
=>분할표 이용
-각 범주나 범주의 list 를 인덱스와 컬럼에 배치해서 사용
-crosstab 이나 pivot_table 함수를 이용
-pivot_table 을 많이 이용하는데 이유는 피봇 테이블은 aggfunc라는 매개변수에 사용하고자 하는 함수를 적용할 수 있기 때문
pivot_table의 매개변수는 index에 컬럼 이나 컬럼의 list 를 설정하고 columns에 동일하게 컬럼이나 컬럼의 list 를 설정하고 aggfunc에 집계에 사용할 함수를 설정
컬럼들이 전부 범주형(명목 척도 와 순서척도)이라면 데이터 개수를 세는 것말고는 의미가 없습니다
-lc.loans.csv 파일을 읽어서 grade 와 status 의 교차 분할 표 작성
result = lc_loans.pivot_table(index='grade',columns='status',aggfunc=lambda x:len(x))
print(result)
4)범주형 과 수치형 데이터 시각화
=>BoxPlot
-pandas 에서 boxplot 이라는 함수를 제공
=>ViolinPlot
-BoxPlot 은 데이터의 범위을 출력하는데는 효율적이지만 밀도 추정 결과를 출력하지 못합니다
-BoxPlot 과 유사하지만 밀도 추정 결과를 두께로 출력
-사각형이나 수염의 개념은 없어서 이상치 탐색에는 적합하지 않음
-이와 유사한 형태로 SwarmPlot (색상을 칠하지 않고 점을 겹치지 않게 출력) 도 있음
-Seaborn의 violinplot이라는 함수를 이용
airline_stats = pd.read_csv("C:\\Users\\User\\Desktop\\python_statistics-main\\python_statistics-main\\data\\airline_stats.csv")
airline_stats.boxplot(by='airline', column ='pct_carrier_delay')
plt.show()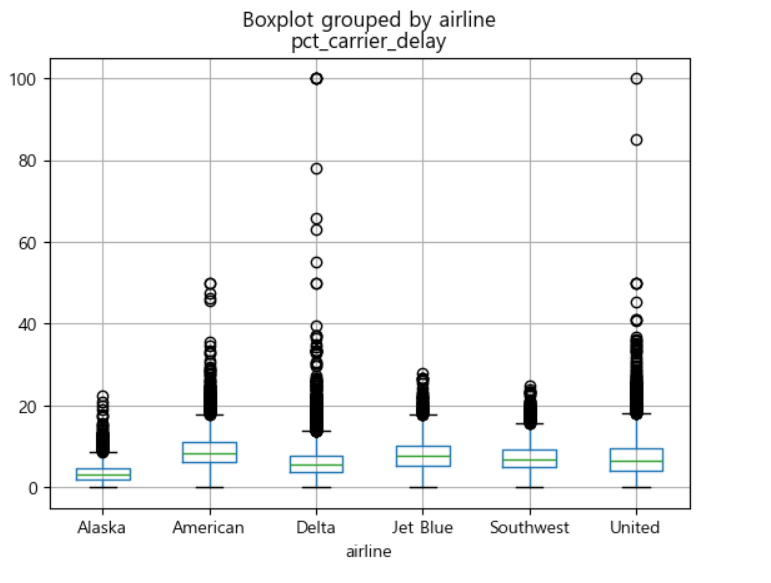
sns.violinplot(data=airline_stats,x='airline', y='pct_carrier_delay')
plt.show()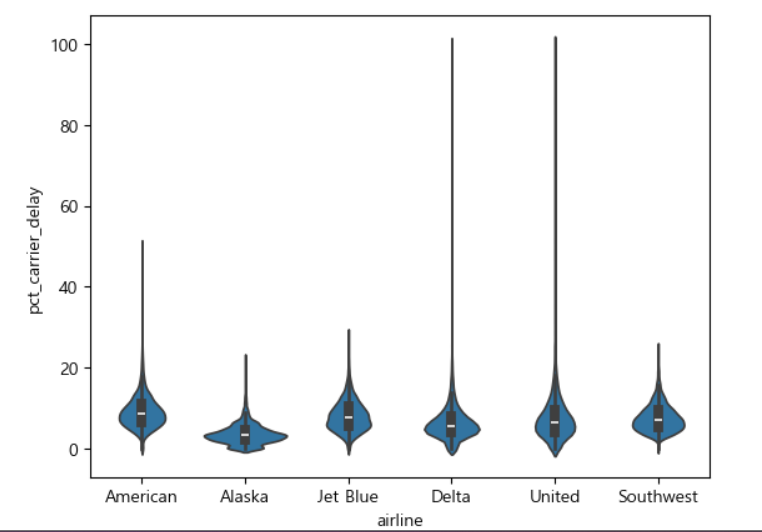
** 확률 분포 모형
1.확률적 데이터와 확률 변수
1)확률적 데이터
=>실험,측정,조사 등을 통해 어떤 데이터 값을 반복적으로 얻는 경우 이 데이터는 누가 언제 얻더라도 항상 동일한 값이 나오는 경우가 있는데 이러한 데이터를 결정론적 데이터라고 하고 혈압 같은 수치는 정확인 예측할 수 없는 값인 나오게 되는데 이러한 데이터를 확률적 데이터라고 합니다
=>대다수 데이터는 확률적 데이터인데 그 이유는 여러 조건이나 상황에 따라 데이터 값이 변할 수 있고 측정시에 발생하는 오차 때문
2) 분포
=>확률적 데이터를 살펴보면 어떤 값은 자주 등장하고, 어떤 값은 드물게 등장하게 되는데 어떤 값이 자주 나오고, 어떤 값이 드물게 나오는지를 나타내는 정보가 분포(Distribution)
=>분포는 범주형 데이터의 경우늑 교차 분할 표나 plot을 직접 이용해서 확인을 하지만 연속형 데이터의 경우는 대부분 binning 을 한 후 히스토그램 등으로 확인
3)확률 분포 함수
=>확률 질량 함수
=>누적 분포 함수
=>확률 밀도 함수
4)확률 질량 함수(PMF)
=>어떤 사건의 확률 값을 이용해서 다른 사건의 확률 값을 계산할 수 있습니다
=>단순 사건은 서로 교집합을 가지지 않는 사건
주사위에서 1,2,3,4,5,6 은 다른 사건과 교집합을 가지지 않으므로 단순 사건
이러한 단순 사건의 확률의 합은 1
=>확률 질량 함수는 각 사건이 발생할 수 있는 확률을 계산해주는 함수
=>확률 질량 함수를 만들 때 위의 사건 처럼 범주형의 형태인 경우는 각 사건의 확률을 명확하게 나타낼 수 있지만 데이터가 연속형의 형태라면 위처럼 나타낼 수 없습니다.
이런 경우에는 구간을 이용하게 됩니다
연속형 데이터에서는 2개의 데이터 사이에 무한대의 데이터가 존재할 수 있기 때문에 하나의 값에 해당하는 확률은 0
둥그런 원반에 화살을 쏴서 특정 각도에 해당하는 확률을 계산
원반에서 0~180 도 사이에 위치할 확률은?


continuous하면 PDF(probability density function), discrete하면 PMF(Probability Massive Function) 이라고 부릅니다.
5)누적 분포 함수
=>주어진 확률 변수가 특정값보다 작거나 같을 확률을 나타내는ㄴ 함수
=>Cumulative Distribution Function

6)분포 추정을 위한 기술 통계값
-평균,중앙값,최빈값
-편차,분산,표준 편차,평균 절대 편차
-범위(Range),순서 통계량(Order Statistics)
7)대칭 분포
=>좌우가 동일한 모양의 분포
=>분포 모양에 따른 평균, 중앙값, 최빈값의 특성
분포가 평균을 기준으로 대칭이면 평균과 중앙값은 일치
분포가 대칭 분포이면 하나의 최대값만을 가지는 단봉 분포이면 최빈값은 평균과 일치
대칭 분포를 비대칭으로 만드는 데이터가 추가되면 평균이 가장 크게 영향 받고 최빈값이 가장 적게 영향 받음
[10,20,30,30,30,40,50]
현재는 평균,중앙값,최빈값이 모두 30
이상치에 영향 받는 순서는 평균 ->중앙값 ->최빈값
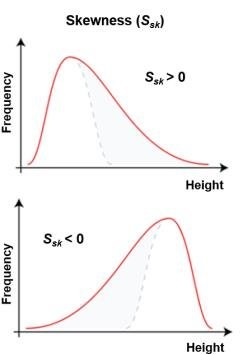
8)표본 비대칭도 -왜도(Skew)
=>평균과의 거리를 세제곱 해서 구한 특징 값
=>표본 비대칭도가 0이면 분포가 대칭
=>표본 비대칭도가 음수이면 표본 평균 값으로 왼쪽에 있는 값을 가진 표본이 나을 가능성이 더 높음
=>표본 비대칭도가 양수이면 오른쪽이 있는 값이 나올 가능성이 높음
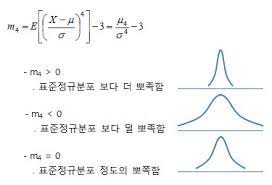
9)표본 첨도(kurtosis)
=>평균과의 거리를 네제곱 해서 구한 특징 값
=>데이터가 중앙에 몰려있는 정도를 정밀 비교하는데 사용
=>정규 분포보다 첨도가 높으면 양수가되면 정규 분포보다 첨도가 낮으면 음수로 정의
10)표본 모멘트
=>k 제곱을 한 모멘트를 k차 표본 모멘트
=>평균을 제곱하지 않았기 떄문에 1차 모멘트라고 하고, 분산은 제곱했기 때문에 2차 모멘트 그리고 skew가 3차 모멘트
첨도는 4차 모멘트
=>scipy.stats 패키지의 skew 나 kurtosis 함수를 이용해서 왜도와 첨도를 구할 수 있고 moment 함수에 데이터와 차수를 설정해서 구할 수도 있습니다
#샘플 데이터 생성
x=np.random.normal(size=1000)
#print(x)
print("표본 평균:",np.mean(x))
print("1차 모멘트:",sp.stats.moment(x,1))
print("표본 분산:",np.var(x))
print("2차 모멘트:",sp.stats.moment(x,2))
#왜도는 중앙을 기준으로 좌우로 펼치는 정도
print("표본왜도:",sp.stats.skew(x))
print("3차 모멘트:",sp.stats.moment(x,3))
#첨도는 정규분포보다 중앙에 값이 몰려있는 정도
#값이 3이면 정규 분포와 동일한 분포
#값이 3보다 작으면 정규 분포보다 꼬리가 얇은 (넓게 펼쳐짐)분포
#값이 3보다 크면 정규분포보다 꼬리가 두꺼운(좁고 뾰족) 분포
#정규분포의 첨도는 3인데, 해석을 편하게 하기 위해서 3을 뺴서 0을 만들기도 함
#excess kurtosis 라고 합니다
print("표본첨도:",sp.stats.kurtosis(x))
print("4차 모멘트:",sp.stats.moment(x,4))
2.확률 분포 함수
1)확률 질량 함수 (PMF)
=>유한 개의 사건이 존재하는 경우 각 단순 사건에 대한 확률만 정의하는 함수
=>사건이 이산적인 데이터
=>소문자 p로 표시
#주사위의 각 눈을 나타내는 수 - 사건
x= np.arange(1,7)
y=np.array([0.1,0.1,0.1,0.1,0.1,0.5])
plt.stem(x,y)
plt.show()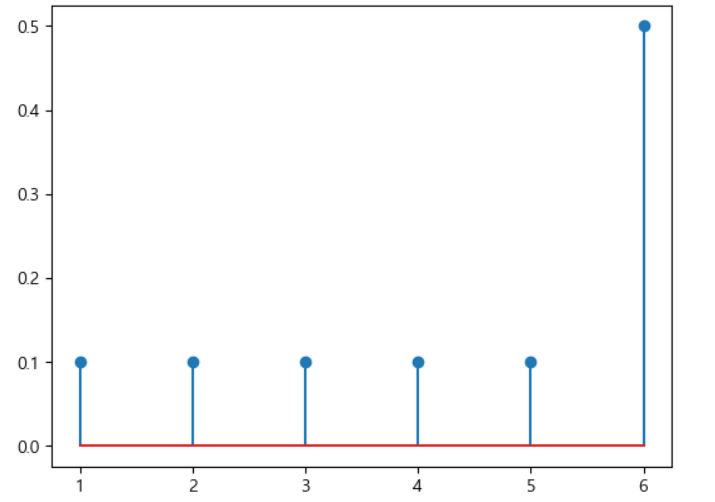
2)확률 분포 함수
=>표본수가 무한대인 경우
-표본의 수가 유한개 일 때는 하나 하나의 사건에 대해서 확률을 정의하면 어떠한 사건에 대해서도 확률을 정의 할 수 있음
표본 공간에 있는 표본 수가 무한대인 경우에는 확률 질량 함수를 이용해서 확률을 정의할 수 없음
회전하는 원반에 화살을 쏘고, 화살이 박힌 위치의 각도를 결정하는 문제에서 정확하게 0도가 될 확률은?
모든 각도에 대해서 가능이 동일하다면 각도가 정확하게 0이 될 확률은 0
-이런 경우는 구간을 이용해서 확률을 정의합니다.
각도가 0도 보다 크거나 30보다 작은 경우의 확률은 정의가 가능한데 확률이 동일하다면 사건이 12개로 유한개로 정의할 수 있기 떄문에 모든 사건에 대해 확률이 동일하다면 1/12 로 정의 가능
=>확률 밀도 함수는 구간에 대한 확률을 정의한 함수
3)누적 밀도(분포) 함수
=>확률 밀도 함수를 정의하기 위해서는 구간을 설정해야 하기 때문에 항상 2개의 값이 필요합니다.
=>하나의 값만을 이용해서 사건을 정의하는 방법을 고안했는데 시작점의 위치를 음의 무한대로 설정하고 하나의 값을 무조건 종료점으로 판정해서 확률을 정의한 함수를 누적 밀도 함수라고 합니다.
=>줄여서 CDF라고 합니다
-음의 무한대에 대한 누적 분포 함수의 값은 0
-양의 무한대에 대한 누적 분포 함수의 값은 1
-입력이 크면 누적 분포 함수의 값은 같거나 커지게 됨
-0에서 시작해서 천천히 증가하여 1로 다가가는 형태
-단조 증가 함수:절대로 내려가지는 않음
3.scipy
1)개요
=>수치 해석 기능을 제공하는 패키지
=>stats 서브 패키지에서 확률 분포 분석을 위한 다양한 기능을 제공
=>확률 분포 클래스
이산 분포
-bernoulli:베르누이 분포
-binom:이항 분포
-moultinomial:다항 분포
연속 분포
-uniform:균일 분포
-norm:정규 분포
-beta
-gamma
-t
-chi2:카이 제곱 분포
-f
-diriclet:디리클레
-multivariate_normal :다변수 정규 분포
2)사용법
-정규 분포 객체 생성: 모수 2개(loc-기댓값,평균,scale-표준 편차)를 가지고 생성
rv =scipy.stats.norm(loc = 1, scale =2) #평균이 1이고 표준편차가 2인 정규 분포 객체 생성
3)확률 분포 객체 함수
-pmf:확률 질량 함수
-pdf:확률 밀도 함수
-cdf:누적 분포 함수
-ppf:퍼센트 포인트 함수, 누적 분포 함수의 역함수
-sf:survival funciton - 생존 함수(1- 누적 분포 함수)
-isf: 생존함수의 역함수
-rvs:랜덤 표본 (샘플 데이터)생성
xx= np.linspace(-8,8,100)
#정규분포 객체 생성
rv=sp.stats.norm(loc =1, scale=2) #평균이 1이고 표준편차가 2인 정규 분포 객ㅊ[
#확률 밀도 함수
pdf = rv.pdf(xx)
plt.plot(xx,pdf)
plt.show()
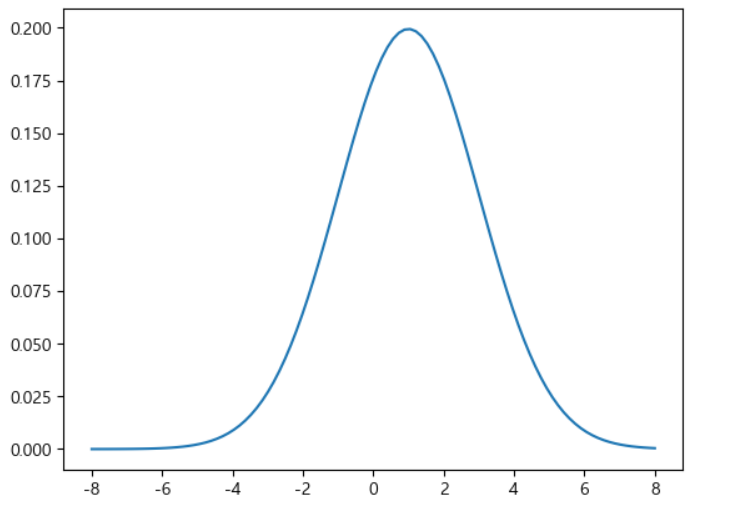
5)정규 분포 객체의 누적 분포 함수
xx= np.linspace(-8,8,100)
#정규분포 객체 생성
rv=sp.stats.norm(loc =1, scale=2) #평균이 1이고 표준편차가 2인 정규 분포 객ㅊ[
#확률 밀도 함수
cdf = rv.cdf(xx)
plt.plot(xx,cdf)
plt.show()
4.확률 분포 모형
1)베르누이 분포
=>베르누이 시행
-결과가 두가지 중 하나로 만 나오는 실험이나 시행을 베르누이 시행
-동전을 던져서 앞면이나 뒷면이 나오는 경우
=>베르누이 확률 변수
-이산 확률 변수:두가지 중에 하나의 경우만 나올 수 있습니다.
-일반적으로 0이나 1로 표기를 하지만 -1이나 1로 표기하기도 합니다
=>베르누이 분포는 1이 나올 확률을 의미하는 모수를 가지게 됩니다.
0이 나올 확률은 1 - (1이 나올 확률)을 하면 나오기 때문에 별도로 정의하지 않습니다
=>scipy.stats.bernoulli 클래스를 이용해서 구현
=>인스턴스를 생성할 때 p 라는 이름으로 분포의 모수를 설정
=>기술 통계값들은 describe()라는 함수를 이용해서 구할 수 있는데 결과는 DescribeResult 타입으로 리턴을 하는데 이 안에 데이터 개수, 최대 ,최소, 평균,분산,왜도,첨도를 순차적으로 저장하고 있습니다.
=>이산 확률 변수를 이용하기 때문에 pmf 사용하는 것이 가능
=>베르누이 분포의 확률 질량 함수를 출력
rv = sp.stats.bernoulli(p=0.7)
#나올 수 경우
xx=[0,1]
#확률질량함수
plt.bar(xx,rv.pmf(xx))
#x축 수정
plt.xticks([0,1],["x=0","x=1"])
plt.show()
=>시뮬레이션- 샘플링
#sample data 생성
#random_state는 seed설정
#seed를 고정시키면 동일한 데이터가 샘플링되고
#seed를 고정하지 않으면 현재 시간 값을 seed로 설정하기 때문에 무작위로 샘플링
#머신러닝에서는 seed를 고정
#동일한 데이터를 샘플링해서 비교를 해야 모델 또는 알고리즘 간의 비교가 가능하기 때
x=rv.rvs(1000,random_state=42)
sns.countplot(x=x,color="green")
plt.show()
=>이론적인 모델과 시뮬레이션 한 결과를 비교
#실제로는 이론과 비교하는 것이 아니고 주장과 비교
#여러차례 시뮬레이션을 한 결과가 비교를 해서 주장이 어느정도 타당성을 갖는지 확인
#시뮬레이션 결과의 비율
y = np.bincount(x,minlength=2) / float(len(x))
print(y)
df= pd.DataFrame({"이론":rv.pmf(xx),"시뮬레이션":y})
df.index=[0,1]
print(df)
2)이항 분포
=>개요
-베르누이 시행을 N번 반복하는 경우에 어떨 떄는 N번 모두 1이 나오고 어떤 경우에는 1이 0번 나올 수도 있는데 이 때 1이 나온 횟수를 X라고 하면 X는 0부터 N까지 가지는 확률변수가 되고 이런 확률 변수를 이항 분포(Binomial Distribution)을 따르는 확률 변수라고 합니다.
- 표본 데이터가 1개이면 베르누이 분포라고하고 표본 데이터가 여러 개이면 이항 분포
=>scipy.stats 서브 패키지의 binom 클래스로 구현
모수가 2개인데 시행횟수 와 1이 나올 확률
시행 횟수를 N이라고 하고 1이 나올 확률을
rv = sp.stats.binom(전체 시행 횟수, 1이 나올 확률)
rv = sp.stats.binom(10,0.5) #1이 나올 확률은 0.5 이고 10번 수행
xx=np.arange(11)
plt.bar(xx,rv.pmf(xx),align='center')
plt.show()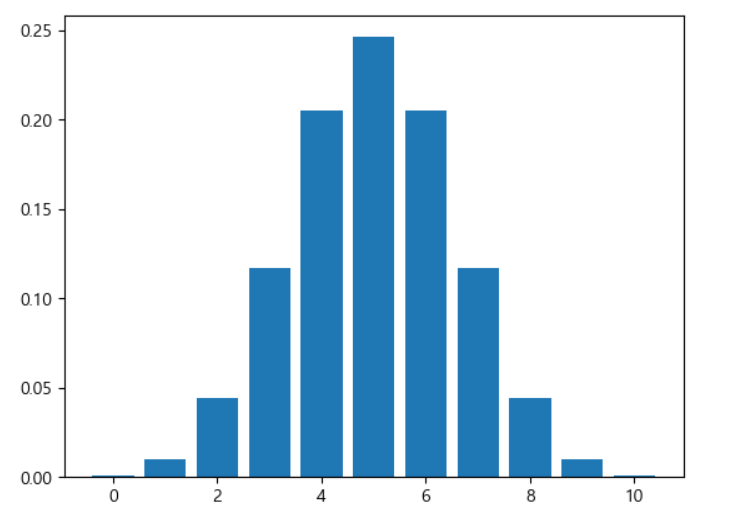
=>앞 뒷면이 나오는 확률이 동일한 동전을 100번 던졌을 때 60회 이상 나올 확률
#해결책
#cdf를 이용:0번부터 나올 확률의 누적 확률
p = sp.stats.binom.cdf(n=100, p=0.5, k=59)
print(1-p)
#sf을 이용: 생존 함수는 누적 분포 함수(cdf의 반대)
p = sp.stats.binom.sf(n=100,p=0.5,k=59)
print(p)
=>동일한 경우에 앞면이 20~60번 나올 확률
p1 = sp.stats.binom.cdf(n=100,p=0.5,k=19)
p2 = sp.stats.binom.cdf(n=100,p=0.5,k=60)
print(p2 - p1)=>퍼센트 포인트 함수 활용: 모수로 구하고자 하는 확률 대입
-함수 이름은 ppf인데 비율을 설정해서 횟수를 구해주는 함수
-동전을 던졌을 때 n회 이상 나올 확률이 80 % 가 넘는 지점은?
p = sp.stats.binom.ppf(n=100,p=0.5,q=0.8)
print(p)
=>베르누이 분포와 이항 분포의 활용-스팸 메일 필터
-모든 메일을 확인해서 스팸으로 가졍할 수 있는 필터의 확률을 구합니다
-각 메일을 단어 단위로 원 핫 이코징을 수행
-각 단어가 스팸메일에 포함된 개수와 스팸 메일에 포함된 개수의 비율을 계산
-현재 메일이 온 경우 메일에 포함된 내용들을 원 핫 인코딩해서 기존에 만들어진 단어들의 스팸 비율을 확인해서 판정
3)카테고리 분포
=>개요
-이항 분포가 성공인지 실패인지를 구별하는 것이라면 카테고리 분포는 2개 이상의 경우 중 하나가 나오는 경우로 대표적인 경우자 주사위
-카테고리는 스칼라 값으로 표현하는 경우가 많지만 확률 변수에서는 카테고리를 원핫 인코딩해서 표현합니다
-원 핫 인코딩을 하는 이유는 편향되지 않게 거리를 동일하게 맞춰 독립적으로 하게 하기 위해서
=>scipy에서는 카테고리 분포를 클래스를 제공하지 않음
다항 분포를 위한 multinomial 클래스에서 시행횟수를 1로 설정하면 카테고리 분포가 됩니다
=>베르누이 분포가 이진 분류 문제에 사용이 되는 것 처럼 카테고리 분포는 다중 분류 문제에 이용
=>모수는 원래 카테고리 개수와 카테고리 별 확률이 되어야 하는데 scipy 을 이용할 때는 1과 각 카테고리 확률의 vector가 됩니다
=>시뮬레이션에 사용되는 데이터는 원 핫 인코딩 된 데이터이어야 합니다
원 핫 인코딩은 pandas 의 get_dummies()을 이용하거나 sklearn.preprocessing 패키지의 Encoder 클래스를 이용해서 수행하는 것이 가능
#카테고리별 확률
mu=[0.1,0.1,0.1,0.1,0.1,0.5]
#카테고리 분포 instance 생성
rv = sp.stats.multinomial(1,mu)
#print(rv)
#데이터 생성
xx=np.arange(1,7)
#원 핫 인코딩 - pandas을 사용해서 pandas 의 자료형
xx_one = pd.get_dummies(xx)
print(xx_one)
print(type(xx_one))
#확률질량함수 출력
#통계,scikit-learn을 이용하는 전처리 그리고 머신러닝에서는
#numpy의 ndarray가 기본 자료형
print(type(xx_one.values))
plt.bar(xx,rv.pmf(xx_one.values))
plt.show()#시뮬레이션 - 여섯번째 열이 1인 경우가 많음
X=rv.rvs(100)
print(X)
4)다항 분포
=>베르누이 시행을 여러 번한 결과가 이항 분포 이듯이 카테고리 시행을 여러 번 한 결과가 다항 분포
=>scipy.stats.multinomial(시행횟수,확률)을 이용해서 인스턴스를 생성합니다.
=>시뮬레이션을 하게 되면 각 카테고리의 횟수가 리턴됩니다
#확률이 동일한 주사위
rv = sp.stats.multinomial(100,[1/6,1/6,1/6,1/6,1/6,1/6])
#10000번 시행
X=rv.rvs(10000)
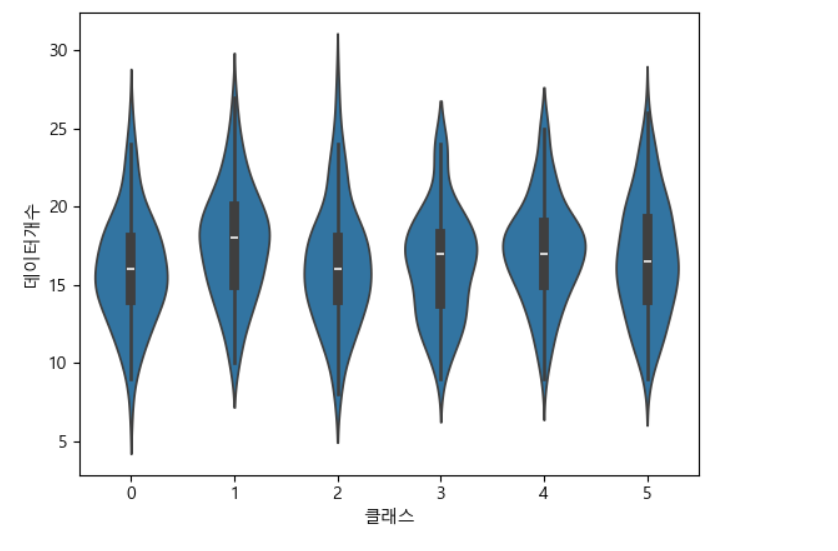
print(X[:20])=>시뮬레이션 결과 시각화
#시뮬레이션 결과 시각화
df = pd.DataFrame(X).stack().reset_index()
df.columns=['시도','클래스','데이터개수']
#print(df)
sns.swarmplot(x='클래스',y='데이터개수', data =df)swarmplot은 시간이 오래 걸림
violinplot으로 변경
'Study > Data전처리 및 통계' 카테고리의 다른 글
| 추론 통계 (1) | 2024.02.26 |
|---|---|
| 확률 분포모형 (1) | 2024.02.23 |
| 기초통계 (0) | 2024.02.21 |
| Pandas(8)-한글 NLP (0) | 2024.02.20 |
| Pandas(7)-Outlier,Encoder,자연어처리 (0) | 2024.02.19 |



