1.추론 통계
1)개요
=>기술 통계가 주어진 데이터의 분포나 빈도, 평균등의 통계량을 이용해서 데이터를 설명하기 위한 목적인 반면 추론 통게의 목적은 주어진 데이터를 이용해서 모집단의 특성을 추론하는 것
=>제한된 데이터로 주어진 실험 결과를 더 큰 과정 또는 모집단에 적용하려는 의도를 반영하는 것을 추론 (inference)라고합니다
2)추론 과정
=>가설을 세움
=>실험을 설계
=>데이터를 수집
=>추론 및 결론을 도출
3)확률 분포의 추정
=>분석할 데이터는 어떤 확률 분포 변수로부터 실현된 표본이라는 가정을 하게 되는데 이것이 데이터 분석의 첫번째 가정
=>확률론적인 관점에서 볼 때 데이터는 확률 변수의 분포를 알아내는데 사용하는 참고 자료일 뿐
4)확률 분포의 결정과정
=>확률 변수가 어떤 확률 분포를 따르는지 알아내는 과정
=>데이터로부터 해당 확률 분포의 모수의 값을 구함
5)데이터의 생성 원리를 알거나 데이터의 특성을 알면 추측할 수 있고 히스토그램을 그려서 확률분포의 모양을 살펴보고 힌트를 얻음
=>데이터가 0 또는 1:베르누이 분포
=>데이터가 카테고리 값 - 카테고리 분포
=>데이터가 0 과 1사이의실수 - 베타 분포
=>데이터가 항상 0 또는 양수 - 로그 정규 분포 , 감마 분포, F 분포, 카이제곱 분포, 지수 분포, 하프코시 분포 등
=>데이터에 크기 제한이 없는 실수 - 정규 분포, 스튜던트 t 분포, 코시 분포, 라플라스 분포 등
=>균일 분포
=>푸아송 분포
=>베이블 분포
6)검정
=>데이터 뒤에 숨어있는 확률 변수의 분포와 모수에 대한 가설의 진위를 정량적으로 증명하는 작업
=>예시)어떤 동전을 15번 던졌더니 앞면이 12번 나왔다 이 동전은 조작되지 않은 동전인지 조작된 동전인지 판단하는것?
=>주식의 수익률이 -2.5 % ,- 5%, 4.3%, -3.7%, -5.6% 일 때 이 주식은 장기적으로 수익을 가져다 줄 것인가 아니면 손실을 가져다 줄 것인가?
7)추정
=>점 추정
-모 집단의 특성을 하나의 값으로 추정하는 방식
#모집단의 특성을 하나의 값으로 추정
fish= pd.read_csv("C:\\Users\\User\\Desktop\\python_statistics-main\\python_statistics-main\\data\\fish_length.csv")
#표본의 평균
mu = sp.mean(fish['length'])
print(mu)
#표본 평균이 4.187이므로 모 평균도 4.187이라고 추정 - 점 추정
-분산이나 표준 편차를 구해서 모집단의 분산이나 표준편차로 추정할 때는 자유도는 데이터 개수 -1 입니다
ddof = (제약조건), dof= (자유도)
=>구간 추정
- 모집단의 특성을 적절한 구간을 이용하여 추정하는 방식으로 하한값과 상한값으로 추정
-용어
신뢰 계수:구간 추정의 폭에 대한 신뢰 정보를 확률로 표현한 것으로 90%,95%,99%을 많이 이용
신뢰 수준: 계산된 구간이 모수를 포함한 확률을 의미하며 90%,95%,99% 등으로 표현
신뢰 구간:신뢰 수준 하에서 모수를 포함하는 구간으로 [하한값, 상한값]으로 표시
표본 오차:모집단에 추출한 표본이 모집단의 특성과 정확히 일치하지 않아서 발생하는 확률의 차이
대통령의 후보의 지지율 여론 조사에서 후보의 지지율이 95% 신뢰 수준에서 표본 오차 플러스 마이너스 3% 범위 내에서 32.4% 으로 조사되었따고 하면 29.4 ~35.4 이내에 존재할 확률이 95%정도 된다는 것이고 5% 수준에선느 틀릴 수 있다는의미
=>가설
-데이터를 특정한 확률 분포를 가진 확률 변수로 모형화를 하면 모수를 추정할 수 있음
-확률 분포에 대한 어떤 주장을 가설(hypothesis)라고 하면 H을 Italic으로 표현
-가설을 증명하는 행위를 통계적 가설 검정이라고 하고 중려서 검정이라고 합니다
-확률 분포의 모숫값이 특정한 값을 가진다는 가설을 검정하는 것을 모수 검정이라고 합니다
-귀무 가설(null hypothesis)
검정 통계 분포를 결정하는 최초의 가설이 귀무 가설
우연에 의해 발생한 것이라는 개념을 구체화하기 위한 논리적 구조
실험에서 얻은 그룹 간의 차이가 무작위로 얻을 수 있는 합리적인 수준과는 극단적으로 다르다라는 증거가 필요한 데 그룹들이 보이는 결과는 서로 동일하면 그룹 간의 우연히 발생한 결과를 기본 가정으로 설정
대다수의 검정의 목적은 귀무 가설이 틀렸다라는 것을 확인하기 위한 작업
-대립 가설(alternative hypothesis)
귀무 가설과 대립되는 가설
귀무 가설이 그룹 A 와 B의 평균에는 차이가 없다라는 것이라면 대립 가설은 그룹 A와 B의 평균에는 차이가 있다라고 봅니다
=>일원 검정(one -way test, single-tailed test - 단측 검정) 과 이원 검정(two -way test, 양측 검정)
-일원 검정
한 방향으로만 우연히 일어날 확률을 계산하는 가설 검정
기존에 사용하던 옵션 과 비교해서 새 옵션이 어떠한지 검정을 하고자 하는 경우 새로운 옵션이 기존의 옵션보다 성능이 좋아야 변경을 할 것이므로 새 옵션이 기존의 옵션보다 성능이 우수하게 평가되는 것이 우연에 의해서 발생한 것이 아니라는 것을 검정해야 하는데 이러한 경우를 단측 검정이라고 합니다
-이원 검정
A와 B는 다르다라는 검정하는 것
-R과 Python의 scipy 은 기본적으로 이원 검정(보수적)을 채택
=>통계적 유의성
=통계학자가 자신의 실험 결과가 우연히 일어나는 것인지 아니면 우연히 일어날 수 없는 것인지를 판단하는 방법
-결과가 우연히 벌어질 수 있는 변동성의 바깥에 존재한다면 이 경우를 통계적으로 유의하다고 판단
-p- value( 유의 확률)을 이용해 판단 :귀무 가설을 구체화한 기회 모델이 주어졌을 떄 관측된 결과와 같이 특이하거나 극단적인 결과를 얻을 확률로 이 값이 낮으면 귀무 가설을 기각하고 대립 가설을 채택
-alpha: 우연에 의한 결과가 능가해야 하는 비정상적인 가능성의 임계확률로 유의 수준이라고 하는데 유의 확률이 유의 수준보다 낮으면 귀무 가설을 기각하고 대립가설을 채택하고 반대의 경우는 귀무 가설을 채택하고 대립가설을 기각
이 값은 분석하는 사람이 결정
- 제 1종 오류: 우연에 의한 결과를 실제 효과라고 판단하는 경우 => 데이터 샘플의 크기를 늘리면 오류 해결
- 제 2종 오류: 실제 효과를 우연에 의한 효과라고 잘못 결론 내리는 경우
-기각역(Critical Value): 유의 수준에 대해서 계산된 검정 통계량
Ex.) 동전을 15번 던졌을 떄 한 쪽면이 12번 나온 경우 이동전을 공정한 동전인가?
- 동전 던지기는 이항 분포 (베르누이 분포) 이고 확률은 0.5
- 이항 분포의 누적밀도함수(cdf)을 이용해서 12번 나올 확률을 찾음
-그런 다음 유의 수준을 설정해서 유의 수준보다 작은 확률이었다면 귀무 가설(이 동전은 공정하다)을 기각하고 만일 나은 확률이 유의 수준보다 크다면 이 경우는 귀무 가설을 채택
비교를 할 때 단축 검정의 경우는 (1 - 누적밀도 함수의 결과)를 선택하면 되지만 양측 검정의 경우는 이 값에 2를 곱해야합니다
#동전 던지기는 앞면과 뒷면이 나오는 이항 분포
#확률(기댓값)은 0.5
#귀무 가설:앞면과 뒷면이 나올 확률은 일치한다.
#이 동전은 공정하다
#대립 가설: 앞면 과 뒷면이 나올 확률은 일치하지 않는다.
#이 동전을 공정하기 않다
N=15 #시행횟수
mu =0.5 # 1이 나올 확률
rv = sp.stats.binom(N,mu)
#축 설정을 위한 데이터
xx = np. arange(N + 1)
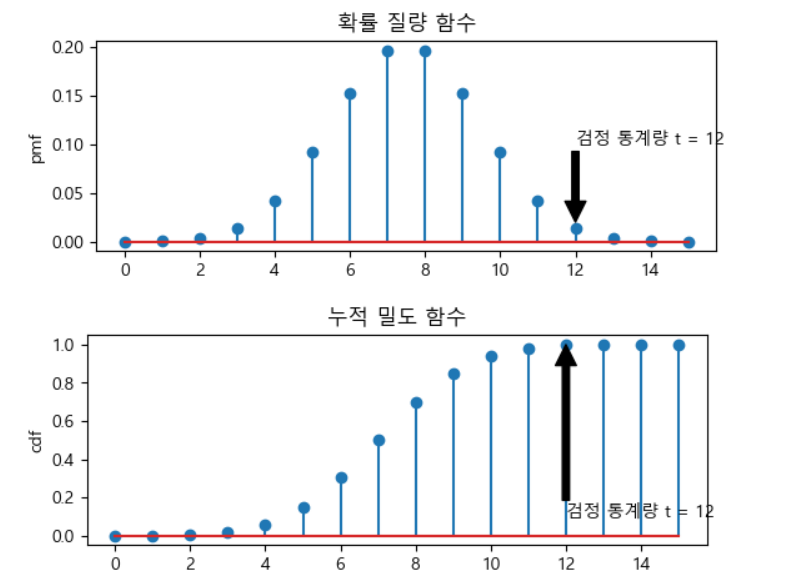
#확률질량함수(pmf) - 이산 확률 분포에서 각 사건이 발생할 확률을 계산해주는 함수
#그래프를 2행 1열로 표시하고 첫번쨰 영역에 표시
plt.subplot(211)
#이산 확률 질량 함수와 누적 밀도 함수는 stem 으로 시각화
plt.stem(xx,rv.pmf(xx))
plt.ylabel('pmf')
plt.title('확률 질량 함수')
plt.annotate('검정 통계량 t = 12', xy= (12,0.02), xytext = (12,0.1),arrowprops= {'facecolor':'black'})
plt.show()
#이산 확률 질량 함수와 누적 밀도 함수는 stem 으로 시각화
plt.subplot(212)
plt.stem(xx,rv.cdf(xx))
plt.ylabel('cdf')
plt.title('누적 밀도 함수')
plt.annotate('검정 통계량 t = 12', xy= (12,1), xytext = (12,0.1),arrowprops= {'facecolor':'black'})
plt.show()
N=15 #시행횟수
mu =0.5 # 1이 나올 확률
rv = sp.stats.binom(N,mu)
#양측 검정에서 사용할 유의 확률: 11번 까지 나올 수 있는 확률을 1에서 빼면 됩니다
p = 2*(1-rv.cdf(12-1))
print(p)
#우연히 12번이상 나올 확률은 0.035(대략 3.5% 정도)
#유의 수준을 5 % 정도로 설정하면 이 경우는 귀무 가설이 기각 - 이 동전은 공정하지 않다
#유의 수준을 1%로 설정하면 이 경우는 귀무 가설을 기각할 수 없음 - 이 동전은 공정한 동전
#단측 검정 - 앞 면이 12번 이상 나왔을 때 이 동전은 앞 면이 더 많이 나오는 동전인가?
#단측 검정 - 앞 면이 12번 이상 나왔을 때 이 동전은 앞 면이 더 많이 나오는 동전인가?
#어떤 분포 - 이항 분포
#1이 나올 확률 - 0.5
N= 15
mu = 0.5
rv = sp.stats.binom(N,mu)
p = (1 - rv.cdf(11)) # 11인 이유는 앞면이 11번까지 나올 확률에서 1 빼면 12번 이상 나올 확률
print(p)
#이제 유의 확률을 계산했으므로 유의 수준을 설정해서 판정
if 0.01 < p:
print("유의 확률이 더 높으므로 귀무 가설 채택")
else:
print("유의 확률이 더 낮으므로 대립 가설 채택").
2.이항 검정
1)A/B 검정(A/B TEST)
=> 두 처리 방법 또는 제품 중 어느 쪽이 다른 쪽보다 더 우월하다는 것을 입증하기 위해서 실험 군을 두그룹으로 나누어 동시에 진행하는 실험
=>두 그룹 중 하나는 기준이 되는 기존 방법이거나 아무런 조치도 취하지 않은 방법이 되는데 이를 대조군이라고 하고 반대뇌는 실험을 하는 집단이나 그룹을 처리군이라고 합니다.
새로운 처리법을 적용하는 처리군이 대조군보다 더 낫다는 것이 대립가설이 됩니다.
=>디자인 이나 마케팅 분야에서 일반적으로 사용되는 방식
=>웹 전환율을 A/ B 테스트로 검정하고자 하는 경우 부트스태핑 방식 같은 방식을 추가적으로 도입해야함.
웹의 전환율을 굉장히 낮기 때문에 하나의 실험 결과만을 가지고 판정하기는 어렵습니다.
2)이항 검정 API
=>scipy.stats.binom_test(검정통계량 -1 이 나온 횟수, n = None -시도 횟수, p =0.5 - 1이 나올 확률, alternative='two-sided'-단측 검정을 하고자하면 less 또는 greater 를 설정)
=>이항 검정은 이산 이라서 직접 연산을 수행해서 판정하는 것이 어렵지 않아서 이 API를 사용하지 않고 , 누적 확률 분포 함수 나 질량 함수를 이용해서 직접 판정하는 경우도 많습니다
=>어떤 게임에서 내가 이길 확률이 0.3인데 100번 했을 때 60번 이상 이기는 것이 가능한지 유의 수준 5%로 검정
#CDF을 이용해서 59번 이길 확률을 빼주면 60번 이상 이길 확률이 만들어짐
p = 1-sp.stats.binom(100,0.3).cdf(59)
print(p)
if p > 0.05:
print("귀무 가설을 기각 할 수 없어서 이런 결과가 나올 수도 있습니다.")
else:
print("귀무 가설을 기각하고 대립가설을 채택해 이런 결과가 나올 확률은 극히 희박")=>tips 데이터셋에서 sex가 Female 인 데이터(여성)에서 비흡연자가 흡연자 보다 많다고 할 수 있는가?
(단,흡연 비율은 50%라고 가정하고 유의 수준 10% 로 검정)
3.T 검정
1)개요
=>모집단의 분산을 모를 때 표본으로 추정하여 평균의 차이를 알아보는 검정
=>검정 통계량으로 스튜던트 t 분포를 가진 통계량을 사용
=>표본 평균의 분포를 근사화하기 위해서 개발
=>최대 2개의 집단까지 비교가 가능
=>T검정은 다음 조건을 만족해야 합니다.
- 연속형 데이터
-랜덤 표본 데이터
-모집단의 분포가 정규 분포에 유사
-분산에 동질성이 있음
=>종류
-1 표본 T 검정 - 평균을 검정
-종속 표본 T 검정 - 한 집단에 두 개의 평균을 비교 (데이터 개수가 같아야 함)
-독립 표본 T 검정 - 서로 다른 집단의 평균을 비교(데이터 개수 상관 없음)
2) 단일 표본 T 검정
=>정규 분포의 표본에 대해서 기대값(평균)을 조사하는 검정 방법
=>API
scipy.stats.tttest_1samp(데이터,popmean -기댓값 (필수), alternative = ' two- sided')
popmean은 귀무 가설의 기댓값
=>기본적인 귀무 가설은 데이터의 평균이 popmean 이므로 대립 가설은 데이터의 평균이 popmean과 다르다
p-value는 이 데이터의 평균이 popmean일 확률
=>이 검정에서 데이터의 개수는 많은 영향을 미치게 됩니다
데이터의 개수가 작으면 제 1유형의 오류가 발생할 가능성이 높습니다.
=>데이터 개수에 따른 T 검정
N = 10
mu_0 = 0
np.random.seed(0)
#정규 분포를 따르고 평균이 0인 샘플데이터 10개 추출
x = sp.stats.norm(mu_0).rvs(N)
p = sp.stats.ttest_1samp(x,popmean = 0)
print(p) #유의 확률이 0.0478
#유의 수준이 5% 라면 귀무가설이 기각
#유형 1의 오류 - 귀무가설이 맞는데 귀무가설이 기각되는 경우 - 샘플 데이터가 적어서
N = 1000
mu_0 = 0
np.random.seed(0)
#정규 분포를 따르고 평균이 0인 샘플데이터 1000개 추출
x = sp.stats.norm(mu_0).rvs(N)
p = sp.stats.ttest_1samp(x,popmean = 0)
print(p) #유의 확률이 0.147
#유의 수준이 5% 라면 귀무가설이 기각
#유형 1의 오류 - 귀무가설이 맞는데 귀무가설이 기각되는 경우 - 샘플 데이터가 적어서
#유형 1 해결방법 - 데이터 증강
=>평균에 대한 검정과 신뢰 구간 구하기
#신뢰구간 구하기위해서 t 분포를 생성
t_ = sp.stats.t(len(data)-1)
#0.975 되는 지점의 좌표를 찾기 - 양쪽 검정이므로
p_05 = t_.ppf(0.975)
data_mean = data.mean()
data_std = data.std(ddof =1)
lp = data_mean - p_05 *(data_std /np.sqrt(len(data)))
hp = data_mean + p_05 *(data_std /np.sqrt(len(data)))
print(f'유의수준 0.05 일 때 신뢰구간[{lp} ,{hp}]')
=.단측 검정
데이터를 측정한 결과 :74,73,75,73,75,74,73,73,74,72
신뢰구간 95%(유의수준 -5%)에서 평균이 73보다 작다고 할 수 있는지 검정
이 경우에는 alternative 인자를 less 나 greater 로 설정하면 단측 검정을 수행
#데이터를 측정한 결과:
data= np.array([74,73,75,73,75,74,73,73,74,72])
mean =73
_, p = sp.stats.ttest_1samp(data, mean, alternative ='less')
#print(p)
if p > 0.05:
print("귀무가설을 기가할 수 없다. 평균은 73이다")
else:
print("귀무가설을 기갈 할 수 있다. 평균은 73보다 작다.")
3)대응(종속) 표본 T 검정
=> 동일한 표본에 대해서 관측된 결과의 기댓값이 같은지 검정
실제로는 대부분의 경우 기댓값이 다르다라는 것을 확인하기 위해서 수행
=>예시
어떤 학생들이 특강을 수강하기 전과 수강한 이후에 대해서 시험을 치뤘을 떄 학생들의 점수 변화가 있었는지?
어떤 약을 복용하기 전과 후가 달라졌는지 확인?
=>API - ttest_1samp
# 귀무 가설: 2집단의 평균이 같다
#대립 가설: 2집단의 평균이 다르다
x1 = np.array([0.7, -16, 0.2])
x2 = np.array([1.7, -0.6, 1.2])
_,pvalue = sp.stats.ttest_rel(x1, x2)
if pvalue > 0.05:
print("귀무 가설을 기각 X. 두집단의 평균은 같다.")
else:
print("귀무 가설을 기각. 두집단의 평균은 다르다.")
=>당뇨약 복용전과 복용후 검정
-동일한 환자에 대한 측정치라고 가정:대응 t 표본 검정
변화가 있는지는 양측검정
밑은 데이터의 평균이 더 작은지 검
# 데이터
#data_b 의 평균이 더 작은지 검정
data_a = np.array([440,90,120,220,230,320,450,180])
data_b = np.array([220,80,100,110,180,250,350,170])
#단측 검정 수행
#앞의 데이터가 더 커야 하면 greater 더 작아야한다면 less
_, p =sp.stats.ttest_rel(data_a,data_b, alternative ="greater")
#단측 검정의 p-value 값이 양측 검정의 p-value /2 입니다
print(p)
if p > 0.05:
print("귀무 가설을 기각할 수 없다. 첫번쨰 데이터가 더 크지 않다.")
else:
print("귀무 가설을 기각한다. 첫번째 데이터의 평균이 더 크다라고 할 수 있다.")
3)독립 표본 t 검정
=>두개의 독립적인 정규 분포에서 나온 두 개의 데이터 셋을 사용해서 두 정규 분포의 기댓값(평균)이 동일한지를 검사
=>scipy.stats.ttest_ind(a,b,axis-0,equal_var=True,alternative='two-sided' ..)
equal_var 옵션은 2개 데이터의 분산이 같은지를 설정하는 옵션
=>이 경우에도 샘플 데이터의 개수가 너무 적으면 제 2종 오류가 발생할 수 있음(실제 효과를 우연에 의한 효과라고 잘못 결론 내리는 것 - 대립 가설을 채택해야 하는데 귀무 가설을 채택하는 경우)가 발생할 수 있음
np.random.seed(0)
N_1 =10
mu_1=0
sigma_1= 1
#두번째 데이터
N_2=10
mu_2=0.5
sigma_2=1
#2개의 데이터 집단의 평균은 0과 0.5로 다름
x1 = sp.stats.norm(mu_1,sigma_1).rvs(N_1)
x2 = sp.stats.norm(mu_2,sigma_2).rvs(N_2)
#그래프로 출
ax = sns.distplot(x1,kde=False, fit=sp.stats.norm,label='1번 데이터 집합')
ax = sns.distplot(x2,kde=False,fit=sp.stats.norm, label='2번 데이터 집합')
ax.lines[0].set_linestyle(":")
plt.legend()
plt.show()
print(sp.stats.ttest_ind(x1,x2,equal_var=True))
#pvalue 가 0.683 이므로 귀무가설을 기각할수 없음
#2 집단의 평균은 같다
#자유도가 18이 나온 것은 데이터 집단이 2개이므로 각각 1개씩 뺴면 18
#실제 평균은 0 과 0.5인데 다른데 같다고 판정
#2종 오류 발생
print(np.mean(x1),np.mean(x2))
print(sp.stats.ttest_ind(x1,x2,equal_var=True))데이터의 크기가 너무 적어서 그러기 떄문에 N의 크기를 키우면 귀무가설을 기각 할 수 있음.
=>샘플의 개수가 많지 않으면 제 2종 오류가 발생할 가능성이 높아짐
4)등분산 검정
=>독립 표본 t 검정에서는 기댓값이 같은지 확인을 하고자 하는 경우 분산의 값이 다른지 같은지를 알아야함
분산이 같은지 다른지 항상 확인해야함
=>등분산 검정에는 bartlett , fligner, levene 검정을 이용하는데 sp.stats 패키지에서 함수를 제공
2개 데이터의 집단만 대입하면 p-value 값을 얻어낼 수 있습니다.
equal_var 을 볼 때 만들어진 데이터를 보고 만들어냄
N1 = 100
N2 = 100
sigma_1 = 1
sigma_2 = 1.2
np.random.seed(0)
x1 = sp.stats.norm(0, sigma_1).rvs(N1)
x2 = sp.stats.norm(0, sigma_2).rvs(N2)
ax = sns.distplot(x1, kde=False, fit=sp.stats.norm, label="1번 데이터 집합")
ax = sns.distplot(x2, kde=False, fit=sp.stats.norm, label="2번 데이터 집합")
ax.lines[0].set_linestyle(":")
plt.legend()
plt.show()

4.윌콕슨의 부호순위
대응 표본 차이에 정규분포를 적용할 수 없는 경우(비모수) 사용하는 중앙값의 차이에 대한 검정
차이의 절대값을 이용해서 순위를 부여
부여된 순위레 평균의 차이와 +,- 부호를 부여해서 곱한후 얻어진 2개의 값의차이를 가지고 판적ㅇ
차이가 있는 경우에는 순위의 편차가 심할것이고, otherwise, 순위의 편차가 별로 없음
차이에 편향이 있을수록 순위에도 편향이 생기고 검정 통계량은 작은 값이 되서 중앙값에 차이가 있다고 주장 가능
scipy.stats.wilcoxon
=>이함수를 이용하면 중간에 표준화 수행 및 정규분포로 검정을 하므로 직접 구현하는 경우와 값이 다름
training_rel = pd.read_csv('c:\\data_all/training_rel.csv')
# print(training_rel.head())
# 알고리즘 이해를 위해 데이터의 개수 줄임
toy_df = training_rel[:6].copy()
print(toy_df)
# 차이
diff = toy_df['후'] - toy_df['전']
toy_df['차'] = diff
print(toy_df)
# 순위
rank = sp.stats.rankdata(abs(diff).astype(int))
toy_df['순위'] = rank
print(toy_df)
# 차이가 적은 데이터의 순위가 앞순위
# 차이가 많은 데이터의 순위가 후순위
# 차이가 음수인 데이터의 순위합과 차이가 양수인 데이터의 순위합을 구함
r_minus = np.sum((diff < 0) * rank)
r_plus = np.sum((diff > 0 ) * rank)
# 낮은 쪽이 검정 통계량
print(r_minus, r_plus)
print('검정 통계량: ', r_minus)
# 이 값이 임계값보다 작은 경우 귀무 가설이 기각되는 단측 검정5.Mann-Whitney Rank Test
1)개요
=>대응되는 표본이 아닌 독립 표본인 경우 정규 분포를 가정할 수 없는 경우 중앙값의 차이에 대한 검정
=>정규 분포가 아니라면 평균이나 분산을 가정할 수 없어서 평균을 사용하지 못하고 중앙값을 사용
=>윌콕슨의 부호 순위 합 검정은 대응 되는 표본이라서 각 열에서 순위를 구하고 순위의 변화량을 측정하는데 전체 데이터를 가지고 순위를 구한 후 각 열의 순위 합을 가지고 검정
6.분산 분석
1)개요
=>여러 그룹의 수치 데이터를 비교해서 여러 그룹 간의 통게적으로 유의미한 차이를 검정하는 통계적 절차가 분산 분석 또는 ANOVA
=>3가지 조건이 필요
-정규성: 각각의 그룹에서 변인은 정규 분포
-분산의 동질성: 모집단의 분산은 각각의 모집단에서 동일
-관찰의 독립성: 각각의 모집단에서 크기가 각각인 표본들이 독립적으로 표집
=>용어
-쌍별 비교: 여러 그룹 중에서 두 그룹 간의 가설 검정
-총괄 검정: 여러 그룹 평균들의 전체 분산에 대한 단일 가설 검정
-분산 분해: 구성 요소를 분리하는 것으로 전체 평균, 처리 평균, 잔차 오차로부터 개별 값들에 대한 기여
-F 통계량: 그룹 평균 간의 차이가 랜덤 모델에서 예상한느 것보다 벗어나는 정도를 측정하는 표준적인 통계량
-SS(Sum of Squares):어떤 평균으로부터의 편차들의 제곱합
2)분산의 중요성
=>어떤 그룹 사이에 평균이 같다고 해서 2그룹 사이에 연관성이 있다고 말하기는 어려움
분산이 다르면 분포는 완전히 달라지기 떄문
그룹과 그룹을 비교할 떄는 평균과 분산을 모두 확인해야 함
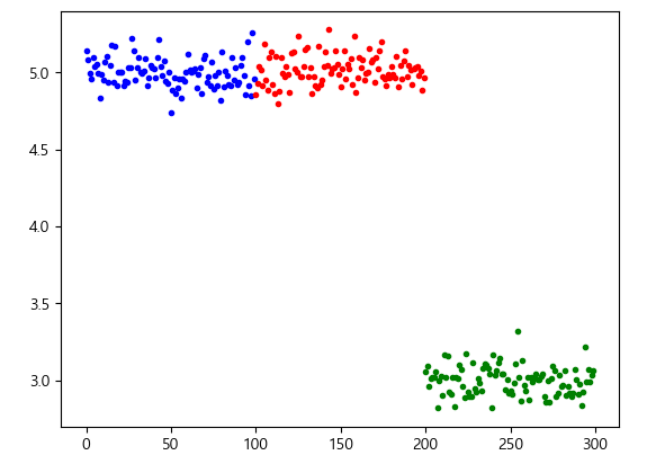
#중앙점의 좌표 - 평균
centers =[5,5,3,4,5]
#표준편차- 분산의 제곱근
#0.1과 2.0 으로 변경헀을때 분포가 아예 달라짐
#0.1인 경우 2개의 분포가 상단에 배치, 1개의 분포가 하단에 배치
#2인 경우 3개의 분포가 동일선상에 배치됩니다
std = 0.1
#std=2.0
colors = 'brg'
data_1 =[]
for i in range(3):
data_1.append(sp.stats.norm(centers[i],std).rvs(100))
plt.plot(np.arange(len(data_1[i]))+ i*len(data_1[0]),data_1[i],'.',color=colors[i])

=>결과
-분산이 클수록 집단의 평균값의 차이는 무의미
-집단 평균 값의 분산이 클수록 집단 내 분산이 작아질수록 평균의 차이가 분명해짐
=>집단 간 분산과 집단 내 분산이 두가지를 이용해서 분석을 하는 것이 분산 분석 - 가장 기본적인 클러스터링(그룹화-집단 내의 분산은 작게 집단과 집단의 분산은 크게)을 할 때 원리
=>분산 분석에서는 일원 분산 분석(종속 변인이 1개이고 독립 변인의 수도 1개)과 이원 분석(독립 변인의 수가 2개이상)으로 나눔
3)일원 분산 분석
=>종속 변인이 1개이고 독립 변인의 집단도 1개인 경우
=>한가지 변수의 변화(독립 변인)가 결과 변수(종속 변인)에 미치는 영향을 알아보기 위해서 수행
=>Python에서는 One-Way ANOVA 분석은 scipy.stats 나 statsmodel 라이브러리 이용
statsmodel을 이용하는 것이 더 많은 분석 정보를 얻어낼 수 있음
=>Altman 910 데이터
-22명의 심장 우회수술을 받은 환자를 3개의 그룹으로 분류해서 시술한 결과
그룹 1 - 50% 아산화 질소와 50 % 산소혼합물을 24시간동안 흡입
그룹2 - 50% 아산화 질소와 50% 의 산소 혼합물을 수술받는 동안만 흡입
그룹3 - 35~50%의 산소만 24시간 동안 흡입
-적혈구의 엽산 수치를 24시간이후에 측정
-적혈구의 엽산 수치가 종속 변인이 되고 3개의 그룹으로 나눈 변인이 독립 변인
-독립 변인에 따른 종속 변인의 평균에 차이가 있는지 검정
p-value가 유의 수준보다 낮으면 평균에 차이가 있는 것이고 그렇지 않으면 평균에 차이가 없다라고 판정
=>사용가능한 API는 scipy.stats.f_oneway(그룹별 데이터를 설정) 와 statsmodels.formula.api 를 이용(R의형태를 갖는 API)
여러 개의 컬럼을 설정할 때 python은 컬럼 이름의 list 를 이용하지만 R은 종속 변인과 독립 변인을 설정할 때 ~ 로 구분해서 설정
#Altman 910 데이터 가져오기
#텍스트의 파일의 내용을 가지고 numpy의 ndarray 생성
#대부분의 경우 pandas을 이용해서 데이터를 읽어오고ndarray 로 변환하지만
#텍스트 데이터(.txt, tsv, csv) 의 경우는 데이터를 가지고 직접 ndarray 생성 가능
import urllib.request
from scipy import stats
# url로 데이터 얻어오기
url = 'https://raw.githubusercontent.com/thomas-haslwanter/statsintro_python/master/ipynb/Data/data_altman/altman_910.txt'
data = np.genfromtxt(urllib.request.urlopen(url), delimiter=',')
# Sort them into groups, according to column 1
group1 = data[data[:,1]==1,0]
group2 = data[data[:,1]==2,0]
group3 = data[data[:,1]==3,0]
# 시각화를 통해서 데이터의 분포 확인
#중앙값의 위치나 박스와 수염의 크기가 거의 비슷하다면 데이터에 차이가 없다라고 판단
plot_data = [group1, group2, group3]
ax = plt.boxplot(plot_data)
plt.show()
# scipy.stats으로 일원분산 분석
F_statistic, pVal = stats.f_oneway(group1, group2, group3)
print('Altman 910 데이터의 일원분산 분석 결과 : F={0:.1f}, p={1:.5f}'.format(F_statistic, pVal))
if pVal < 0.05:
print('p-value 값이 충분히 작음으로 인해 그룹의 평균값이 통계적으로 유의미하게 차이납니다.')
else :
print('p-value 값이 충분히 작지 않으므로 인해 그룹의 평균값이 통계적으로 유의미하게 차이나지 않습니다.')

#statsmodels API 활용
from statsmodels.formula.api import ols
df = pd.DataFrame(data, columns=['value', 'treatment'])
model = ols('value~C(treatment)',df).fit()
import statsmodels.api as sm
print(sm.stats.anova_lm(model))
print(type(sm.stats.anova_lm(model)))
4)이원 분산 분석
=>독립 변인의 수가 2개 이상일 때 집단 간 차이가 유의한지를 검증
=>Interaction Effect를 확인하기 위해 사용
한 변인의 변화가 결과에 미치는 영향이 다른 변인의 수준에 따라 달라지는 가를 하는 것을 확인
=>altman _12_6
-태아 머리 둘레 측정 데이터
-4명의 관측자가 3명의 태아를 대상으로 측정
inFile = 'altman_12_6.txt'
url_base = 'https://raw.githubusercontent.com/thomas-haslwanter/statsintro_python/master/ipynb/Data/data_altman/'
url = url_base + inFile
#첫번째 열이 머리 둘레 크기-종속 변인
#두번쨰 열이 태아를 구별하기 위한 번호-독립 변인
#세번째 열이 관측자를 구별하기 위한 번호-독립 변
data = np.genfromtxt(urllib.request.urlopen(url), delimiter=',')
# 이원 분산 분석
df = pd.DataFrame(data, columns=['head_size', 'fetus', 'observer'])
# df.tail()
# 태아별 머리 둘레 plot 만들기
df.boxplot(column = 'head_size', by='fetus' , grid = False)
#훈련을 수행하고 결과를 확인
from statsmodels.formula.api import ols
formula = 'head_size ~ C(fetus) + C(observer) + C(fetus):C(observer)'
lm = ols(formula, df).fit()
print(sm.stats.anova_lm(lm)) #가장 마지막 열의 첫번쨰 데이터가 p-value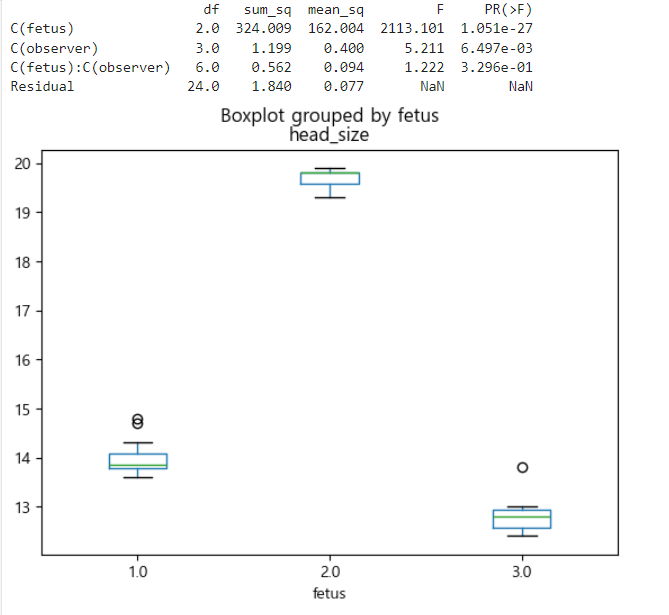
5)웹 점착성
=>웹 전환율
-현재 페이지에서 다른 페이지로 이동하는 비율
-상품 목록 페이지에서 상품 상세 보기 페이지로 이동하는 것 또는 상품 상세보기 페이지에서 상품 결제 페이지로 이동하는 것등의 비율
-포탈의 광고 또는 SNS 광고를 통해서 들어오는 고객의 비율
=>웹 점착성
-방문자가 페이지에서 보낸 시간
-일반적인 이원 분석을 하는 경우는 변인이 2개 이상이고 모든 관측자가 선택권이 없음.
-여러 명의 유저가 여러 페이지에서 보낸 시간을 가진 데이터를 가지고 분산 분석을 수행
-이 데이터가 앞의 데이터와 다른 점은 페이지를 선택하는 권리가 유저에게 있다는 것
모든 유저가 모든 페이지에 방문하는 것은 아니며 그 확률은 매우 낮음
-부트스트래핑이나 순열 검정(재표본 추출) 같은 방식을 이용
모든 데이터를 한 상자에 모아서 페이지 개수 별로 각 페이지의 개수만큼 추출
각 그룹의 평균을 기록한 후 각 그룹의 평균 사이의 분산을 기록
이 작업을 여러 번 반복한 후 이 분산이 관찰된 변화가 p 값
#web page에 머무르는 시간은 웹 점착성이라고 함
#4개의 페이지에 머무르는 시간이 기록된 데이터를 가져오기
four_sessions = pd.read_csv("C:\\Users\\User\\Desktop\\python_statistics-main\\python_statistics-main\\data\\four_sessions.csv")
#print(four_sessions.head())
# 그룹 별 Time데이터의 평균의 분산 구하기
observed_variance = four_sessions.groupby('Page')['Time'].mean().var()
print("그룹별 Time의 평균에 대한 분산:",observed_variance)
#랜덤하게 섞어서 그룹 별로 Time 에 대한 평균의 분산을 구해주는 함수
def perm_test(df):
df=df.copy()
df['Time'] = np.random. permutation(df['Time'].values)
return df.groupby('Page')['Time'].mean().var()
np.random.seed(1)
#3000번 수행해서 observed_variance 보다 분산이 높은 비율을 계산
perm_variance = [perm_test(four_sessions)for _ in range(3000)]
#이 비율의 값이 p-value
#유의 수준을 정해서 분산이 의미가 있는지 판정
#유의 수준보다 p-value 값이 작다면 분산의 차이가 의미가 있습니다.
#점착성의 차이가 있다 - 이 페이지들은 차이를 가져옴
#2개의 페이지를 가지고 이 페이지를 수행하면 A/B테스트
print("p-value:",np.mean([var > observed_variance for var in perm_variance]))
일정 시간이 지나면 cu
'Study > Data전처리 및 통계' 카테고리의 다른 글
| 추론통계 (0) | 2024.02.27 |
|---|---|
| 확률 분포모형 (1) | 2024.02.23 |
| 기술 통계 (0) | 2024.02.22 |
| 기초통계 (0) | 2024.02.21 |
| Pandas(8)-한글 NLP (0) | 2024.02.20 |



