1.균일 분포
1)개요
=>모든 확률에 대해서 균일한 분포를 갖는 모형
=>scipy.stats.uniform 함수로 생성
=>버스의 배차 간격이 일정한 경우
시간표를 모르고 버스 정류장에 나갔을 때 평균 대기 시간은?
=>샘플 생성
rvs(loc=0,scale=1,size=1,random_state=None)
-loc: 기댓값, 평균
-scale:범위라ㅎ고 하는데 표준 편차
-size 은 개수
-random stae 은 seed값
seed값은 여기서 설정하지 않고 numpy을 이용해서 미리 설정한 후 사용해도 됩니다.
=>pmf(확률 질량 함수), pdf(확률 밀도 함수), cdf (누적 분포 함수), ppt(퍼센트 포인트 함수), sf(생존 함수)를 가지고 있습니다
=>균일 분포의 경우 동일한 크기의 구간에 대한 확률이 거의 비슷하지만 2개의 균일 분포 합은 그렇지 않음
2)실습
=>마을에 다니는 버스의 주기는 1시간인 경우:균일 분포
균일분포
스케일:60
-버스 시간표를 모르는 사람이 버스 정류장에 갔을 때 대기시간이 7분 이내일 확률
result = sp.stats.uniform.cdf(scale=60,x=7)
print(result)
2.정규 분포
1)개요
=>가우시안 정규 분포라고도 하는데 자연 현상에서 나타나는 숫자를 확률 모형으로 나타낼 때 가장 많이 사용되는 모형
=>데이터가 평균을 기준으로 좌우 대칭
=>평균을 기준으로 표준편차 1배 내에 약 68 % , 그리고 좌우 2배 안에 약 95% 정도의 데이터가 분포된 경우
=>평균이 0이고 표준편차가 1인 경우를 특별히 정규 분포라고 합니다.
=>scipy의 stats.norm 클래스를 이용해서 구현
2)실습
mu,std=0,1
rv =sp.stats.norm(mu,std)
xx=np.linspace(-5,5,200)
plt.plot(xx,rv.pdf(xx))
plt.ylabel('확률')
plt.title('정규 분포 곡선')
plt.show()
3)붓꽃 데이터의 꽃잎 길이 확인
from sklearn.datasets import load_iris
#load_iris은 붓꽃에 대한 정보를 담은 데이터로 4개의 피처와 붓꽃 종류는 타겟으로 구성
setosa_sepal_length= load_iris().data[:50,2]
#print(setosa_sepal_length)
import seaborn as sns
sns.histplot(setosa_sepal_length,kde=True)
plt.show()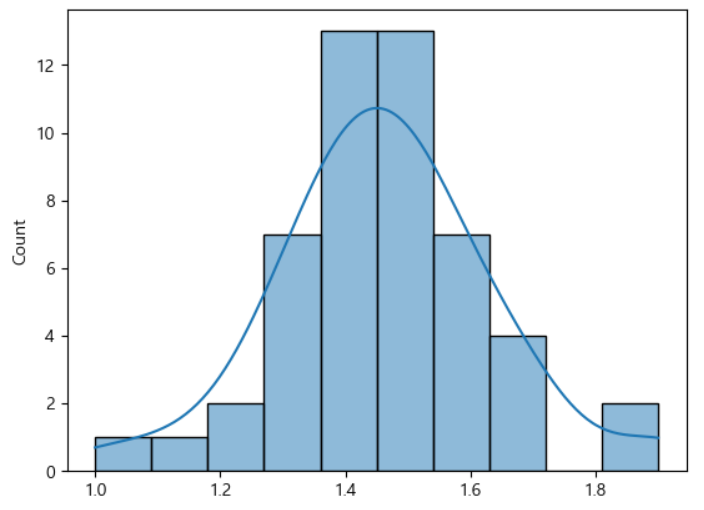
4)finance- datareader 패키지
=>시계열 데이터를 수집해서 DataFrame을 만들어주는 패키지
=>설치:pip install finance-datareader
#삼성전자 주가확인
df=fdr.DataReader('005930','2011-01-01')
print(df.tail())
#코스피 확인
kospi=fdr.DataReader("KS11","2011-01-01")
print(kospi.head())
5)나스닥(IXIC)의 일자별 차이 - 정규 분포와 유사
import pandas as pd
import matplotlib.pyplot as plt
data = pd.DataFrame()
data['IXIC']=fdr.DataReader("IXIC","2011-01-01")["Close"]
#결측치 제거
data = data.dropna()
#시각화
data.plot(legend=False)
plt.show()
6)로그 정규 분포
=>데이터에 로그를 한 값 또는 변화율이 정규 분포가 되는 분포
=>주가의 수익률은 정규 분포 라면 주가 자체는 로그 정규 분포(log -normal distribution)
=>로그 정규 분포를 가지는 데이터는 기본적으로 항상 양수라서 로그 변환을 수행한 다음 사용하는 것이 일반적
어떤 데이터가 로그 정규 분포를 가지는데 이 데이터를 머신러닝이나 딥러닝에 사용하는 경우 로그 변환을 한 후 사용하기도 합니다.
=>로그 정규 분포와 일반 정규 분포 시각화: 로그 정규 분포의 데이터 모양을 기억
# 평균이 1인 분포 데이터 생성
mu = 1
rv=sp.stats.norm(loc=mu)
x1=rv.rvs(1000)
#정규 분포 데이터를 이용한 로그 정규 분포 데이터 생성
#시작하는 부분에 데이터가 치우침
#타겟 데이터가 한쪽으로 몰려있는 경우 로그 변환을 고려
s=0.5
x2=np.exp(s*x1)
sns.histplot(x1,kde=True)
plt.show()
7)Q-Q Plot
=>개요
-정규 분포는 연속 확률 분포 중에서 가장 널리 사용되는 확률 분포라서 어떤 데이터의 분포가 정규 분포인지 아닌지 확인하는 것은 중요한 통계 분석 중 하나
-Q-Q(Quantile -Quantile) Plot은 분석할 표본 데이터의 분포와 정규 분포의 분포 형태를 비교해서 표본 데이터가 정규분포를 따르는지 검사하는 간단한 시각적 도구
-정규 분포를 따르는 데이터를 Q-Q Plot으로 그리면 대각선 방향의 직선 모양으로 만들어집니다.
-정규 분포를 따르지 않은 데이터를 Q-Q Plot 으로 그리면 직선이 아니라 휘어진 모양이 나타나게 됩니다
=>랜덤하게 데이터를 생성해서 Q-Q Plot 을 그리기
#랜덤하게 데이터 추출
x=np.random.rand(1000)
sp.stats.probplot(x,plot=plt)
plt.show()
8)중심 극한 정리
=>모집단이 정규 분포가 아니더라도 표본 크기가 충분하고 데이터가 정규성을 크게 이탈하지 않는다면 여러 표본에서 추출한 평균은 종 모양의 정규 곡선을 따른다
#여러개의 표본에서 추출한 데이터를 합치면 정규 분포와 유사해 진다
xx=np.linspace(-2,2,100)
for i, N in enumerate([1,2,5,10,20]):
X=np.random.rand(5000,N)
Xbar = (X.mean(axis=1) - 0.5) * np.sqrt(12 * N)
sp.stats.probplot(Xbar,plot=plt)
plt.show()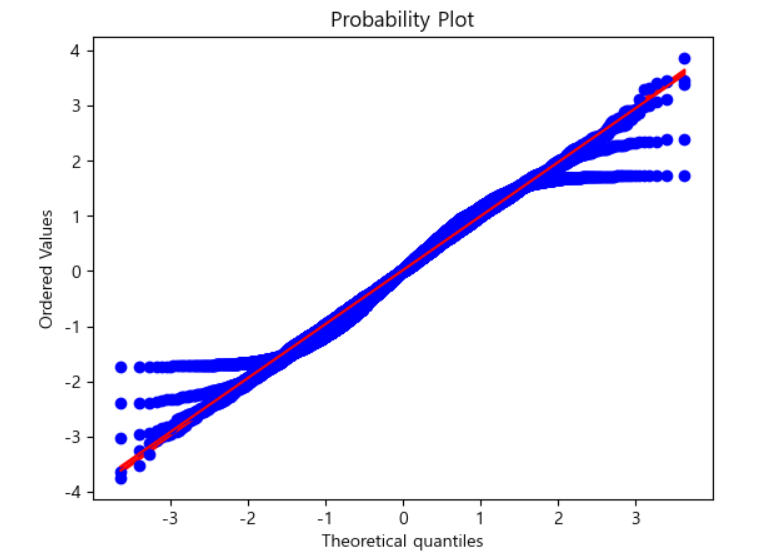
3. t 분포
1)t 분포
=> 정규분포의 표본을 표준 편차로 나눠 정규화 한 z 통계량은 항상 정규 분포
=> z 통계량을 구할려면 표준 편차를 알고 있어야 하지만 현실적으로 표준 편차를 정확히 알 수 없기 때문에 표본에서 측정한 표본 표준 편차를 이용해서 정규화를 수행
=> 정규 분포로부터 얻은 N개의 표본에서 계산한 표본 평균을 표본 평균 편차로 정규화 한 값이 t 통계량
=> 분포를 알 수 없는 샘플 데이터만 주어진 경우에 확률이나 값을 추정할 때 사용
=> 기온을 측정했는데 특정 기온이 확률적으로 몇 %에 해당하는지 알고자 하는 경우?
#수익률의 히스토그램
#수익률
log_returns = np.log(data / data.shift(1))
log_returns.hist(bins=50)
plt.show()
# Q-Q plot
#enumerate 함수는 iterable 객체를 받아서 순회를 하는데
#(인덱스, 데이터)로 리턴해주는 함수
for i,sym in enumerate(symbols):
ax = plt.subplot(2,3,i+1)
sp.stats.probplot(log_returns[sym].dropna(),plot=ax)
#dropna는 국가별 쉬는날이달라서 안맞을 수 있음
#nan 값을 날림
plt.show()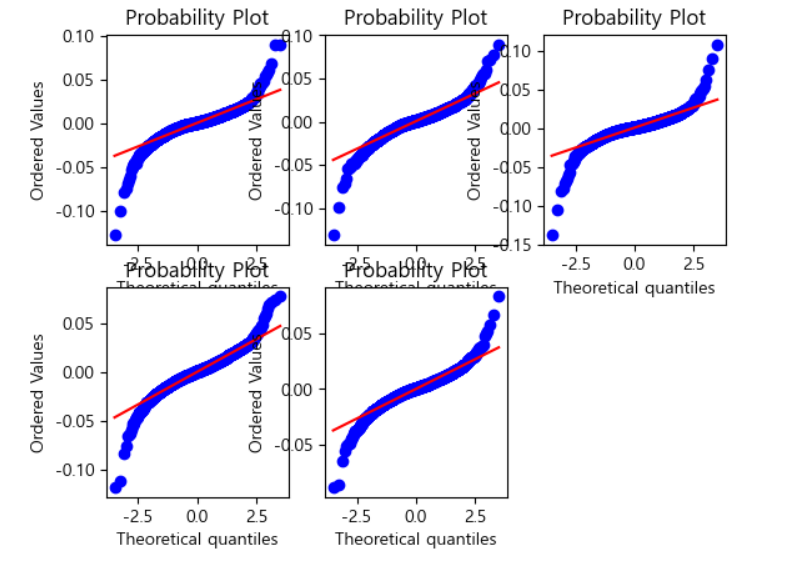
4. 카이 제곱 분포
1) 개요
=> 정규 분포를 따르는 확률 변수 X의 N개 표준의 합은 표본 분산으로 정규화하면 스튜턴드 t 분포를 따름
=> 제곱을 해서 더하면 양수만을 갖는 분포가 만들어지는데 이 분포를 카이 제곱 분포라고 합니다.
=> scipy.stats.chi2 클래스를 이용해서 구현
=> 제곱 합을 구하는 표본의 수가 2보다 커지면 0 보다 큰 어떤 수가 흔하게 발생
5.F 분포
1) 개요
=> 카이 제곱 분포를 따르는 독립적인 두 개의 확률 변수 표본을 각각 x1,x2라고 할 때 이를 데이터의 개수인 N1, N2로 나눈 뒤 비율을 구하면 F 분포라고 합니다.
N1 과 N2는 자유도
=> t 분포의 표본 값을 제곱한 값이 F 분포
2) 특징
=> N1 과 N2 의 값이 같을 경우 1 근처 값이 가장 많이 발생할 것 같은데 실제는 1이 아닌 다른 수가 조금 더 흔하게 발생
=> N1 과 N2 의 값이 커지면 1 근처의 값이 많이 발생
6. 푸아송 분포
1) 개요
=> 단위 시간 안에 어떤 사건이 몇 번 일어날 것인지를 표현하는 이산 확률 분포
=> 푸아송이 민사 사건과 형사 사건 재판에서의 확률에 관한 연구 및 일반적인 확률 계산 법칙에 대한 서문에서 최초로 사용
2) 예시
=> 어떤 식당에 주말 오후 동안 시간당 평균 20명의 손님이 방문한다고 할 때 다음 주 주말 오후에 30분 동안 5명의 손님이 방문할 확률은?
시간당 손님은 20명이므로 30분에는 10명이 방문한다고 기대할 수 있음
(10(기대값)의 5(예측값)승 * e-10승) / 5! = 0.0378
3) poisson 이라는 클래스를 이용해서 구현
=> 단위 시간 당 발생하는 사건의 개수를 설정
4) 분포 시각화 - 단위 시간당 사건이 10개가 발생하는 경우
5) 2022년 기준으로 한 시간 평균 신생아 수는 682명인 경우에는 한 시간에 650명 이하의 신생아를 낳을 확률은?
p = sp.stats.poisson.cdf(mu = 682, k = 650)
print(p)
7. 지수 함수
1)개요
=> 사건이 독립적일 대 일정 시간동안 발생하는 사건의 횟수가 푸아송분포라면 다음 사건이 일어날 때까지 대기 시간은 지수 분포를 따름
=> 사건의 대기 시간이 일정한 형태로 줄어들거나 늘어나는 경우는 weibull distribution을 이용
=> scipy.stats.expon이라는 클래스를 이용해서 구현
scale을 이용해서 시간을 설정
2) 스마트폰의 배터리 수명은 평균 24시간인 경우
=> 스마트폰 배터리가 20시간이내에 소진할 확률은
p = sp.stats.expon.cdf(scale=24, x = 20)
=> 스마트폰 배터리가 12시간에서 30시간 이내에 소진할 확률
=> 소진할 확률이 85%가 되는 지점은?
============================================================================================
** 샘플링 - 표본 추출
1. 전수 조사 와 표본 조사
-> 전수 조사
-모집단 내에 있는 모든 대상을 조사하는 방법
-모집단의 특성을 정확히 반영하지만 시간과 비용이 많이 소모
-> 표본 조사
- 모집단으로부터 추출된 표본을 대상으로 분석을 실시
- 전수 조사의 단점을 보완할 수 있지만 모집단의 특성을 반영하는 표본이 제대로 추출되지 못하는 경우 수집된 자료가 무용지물이 될 수 있음
2. 용어
-> Sample: 큰 데이터 집합으로부터 얻은 부분 집합
-> Population: 데이터 집합을 구성하는 전체
-> N(n): 모집단의 크기
-> 랜덤 표본 추출: 무작위로 표본을 추출하는 것
-> 층화 랜덤 표본 추출: 모집단을 여러 개의 층으로 나눈 후 각 층에서 무작위로 표본을 추출
-> 단순 랜덤 표본 추출: 층화없이 단순하게 무작위로 표본을 추출
-> 표본 편향(Sample Bias): 모집단 잘못 대표하는 표본을 추출하는 것
-> 표준 오차
- 통계에 대한 표본 분포의 변동성
- 표본 표준 편차 - s)/ (표본 크기의 제곱근)
- 표준 오차와 표본 크기 사이의 관계는 n 제곱근의 법칙이라고 하는데 표준 오차를 2배 줄일려면 표본 크기를 4배로 증가시켜야 함
3. 표본 추출
1) 머신러닝에서 표본 추출하는 방법
=> train data(모델을 생성) 와 test data(모델 테스트)로 나누는 방법
=> train data 와 test data 와 validation data로 나누는 방법
2) 복원 추출 과 비복원 추출
=> 복원 추출은 추출된 데이터를 모집단에 포함시켜서 추출
python에서는 random.random,randint, randrange 등의 함수가 있음
=> 비복원 추출은 한 번 추출된 데이터는 모집단에 포함시키지 않고 추출
python에서는 random.sample 함수가 제공됨
=> 복원 추출과 비복원 추출
3) 가중치를 적용한 표본 추출
=> 표본의 비율이 달라져야 하는 경우 표본을 추출할 때 비율을 설정해서 추출하는 것
=> numpy의 random.choice라는 함수를 이용할 수 있습니다.
추출하고자 하는 배열 그리고 개수 그리고 확률을 제시하면 가중치를 적용해서 표본을 추출합니다.
=> 현실 세계의 문제에서는 간혹 가중치를 적용한 표본 추출이 어려우면 표본 추출을 해서 분석을 한 후 가중치를 적용하기도 합니다.
4)pandas 의 표본 추출
=> Series 나 DataFrame
5) scikit-learn.model_selection의 train_test_split()
=> 훈련 데이터와 테스트 데이터를 분할하기 위한 API
=> shuffle 옵션이 있는데 기본값은 True로 되어 있는데 시계열 데이터와 같은 데이터를 추출할 때는 랜덤한 추출을 하면 안되고 순차적 분할을 해야 하는 경우가 있습니다.
이런 경우에는 False 를 설정해서 추출을 해야합니다.
=> 2개의 데이터 배열을 대입해야 하는데 하나의 데이터는 feature 이고 다른 하나의 데이터는 target 입니다.
=> test_size를 이용해서 테스트 데이터의 비율을 설정을 해야합니다.
일반적으로 8:2 또는 7:3을 선호하지만 데이터가 아주 많은 경우에는 5:5를 설정해도 됩니다.
이렇게 데이터가 많으면 테스트 데이터를 다시 테스트 데이터 와 검증을 위한 데이터로 분할하기도 합니다.
=> 리턴되는 데이터는 4개의 데이터 그룹에 대한 tuple 입니다.
피처의 훈련데이터, 피처의 테스트 데이터, 타겟의 훈련 데이터, 타겟의 테스트 데이터
=> 샘플 데이터를 생성
#데이터 생성
#특별한 경우가 아니면 피처는 대문자 x로 나타냅니다.
#타겟은 소문자 y로 나타냅니다.
#numpy의 1차원 ndarray는 출력을 하면 옆으로 펼쳐지지만 하나의 열로 간주합니다.
X = np.arange(20).reshape(10, 2)
print(X)
y = np.arange(10)
print(y)
=> 순차적 분할
#순차적 분할 - 7:3
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, shuffle = False)
print('X_train shape: ', X_train.shape)
print('X_test shape: ', X_test.shape)
print('y_train shape: ', y_train.shape)
print('y_test shape: ', y_test.shape)
print()
print(X_train)
=>층화 무작위 추출
-데이터를 일정한 비율을 적용해서 데이터 추출
-머신러닝에서 타겟을 비율의 일정하지 않은 경우 사용
타겟의 비율이 편차가 심한 경우 랜덤하게 추출했을 떄 비율이 낮은 데이터가 추출이 안될 수도 있고 너무 많이 추출될 수도 있습니다.
이렇게 머신러닝의 결과가 엉뚱한 결과가 추출될 수 있습니다.
-층화 추출을 할 때는 stratify 옵션에 리스트을 대입하면 비율 계산을 해서 추출을 합니다
from sklearn.model_selection import train_test_split
X = np.arange(30).reshape(15,2)
y=np.arange(15)
grep = [0,0,0,0,0,1,1,1,1,1,1,1,1,1,1]
'''
#단순한 방식으로 추출을 하게 되면 한쪽으로 샘플이 쏠리는 현상이 발생하고
X_train, X_test, y_train, t_test = train_test_split(X,y,test_size=0.2,
shuffle=True,
random_state=42)
print(y_train) # 0,1,2,3,4 index 가 다 0 인데 test하는 곳에는 없음
#이렇게 되면 샘플 데이터에서는 잘 맞지만 실제 서비스 환경에서는 제대로 맞추지 못하는
#현상이 발생할 수 있습니다
'''
#stratify 추가
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,
shuffle=True,
stratify=grep,
random_state=49)
print(y_train)
print(y_test)
6)scikit-learn.model_selection 의 StratifiedShuffleSplit()
=> 층화 추출을 수행해주는 API
=>n_splits 이라는 옵션을 이용해서 데이터를 몇 개의 그룹으로 분할할지를 설정
=>데이터를 리턴하지 않고 데이터의 인덱스를 리턴합니다
=>k-folds cross-validation을 수행하기 위해서 만든 API입니다
모델을 만들고 이를 검증 할 때 전체 데이터를 N등분해서 N-1개 그룹으로 모델을 만들고 1개의 그룹으로 테스트를 수행
#교차 검증을 위해서 데이터를 b 등분 층화 추출을 해주는 API
#직접 사용하지 않고 머신러닝 모델이 내부적으로 적용
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits=1,test_size=0.2)
print(split)
for train_idx ,test_idx in split.split(X,grep):
X_train = X[train_idx]
X_test = X[test_idx]
y_train = y[train_idx]
y_test = y[test_idx]
print(y_train)
print(y_test)
7)재표본 추출
=>랜덤한 병동성을 알아보자는 일반적인 목표를 가지고 관찰된 데이터의 값에서 표본을 반복적으로 추출하는 것
=>종류
-순열 검정: 두 개 이상의 표본을 함께 결합해서 관측값을 무작위로 재표본으로 추출하는 방식
-부트스트랩:통계량이나 모델 매개변수의 표본 분포를 추정하기 위해 현재 있는 표본에서 추가적으로 표본을 복원 추출하고 각 표본에 통계량과 모델을 다시 계산하는 과정
8)순열 검정
=>두개 이상의 표본을 함께 결합해서 관측값을 무작위로 재표본으로 추출하는 과정
=>두 개 이상의 표본을 사용하여 A/B 검정(하나의 UI 와 새로운 UI를 도입했을 때 결과 비교 등에 사용하는 방식) 등에 이용
=>과정
1)여러 그룹의 결과를 하나의 데이터 집합으로 합침
2)결합된 데이터를 잘 섞은 다음 A 그룹과 동일한 크기의 표본을 비복원 무작위로 추출
3)나머지 데이터에서 B 그룹과 동일한 크기의 샘플을 비복원 무작위로 추출
-그룹이 더 존재하면 동일한 방식으로 추출
-원래의 표본에 대해 구한 통계량 또는 추정값이 무엇이었든지 간에 추출한 재표본에 대해서 다시 계산하고 기록을 한 다음 원래의 표본에 대해서 구한 값과 비교
-이작업을 여러 번 반복
UI 개선 프로젝트를 진행 할 때 기존 UI 와 새로운 UI 2개를 놓고 load balancer 라는것을 둠으로써 사용자가 들어올 때 load balancer 로 1번과 2번으로 각각보내준다음 평가합니다. UI 개선 프로젝트는 이쁘게 하려는게 아니라 회사에 돈을 가져오게 하려고 하는 것
데이터 분석의 목적) 회사가 돈을 벌 수있는지 없는지를 파악하기 위해 하는 것
9)부트스트래핑
=>모수의 분포를 추정하는 방법으로 현재 있는 표본에서 추가적으로 표본을 복원 추출하고 각 표본에 대한 통계량을 다시 계산하는 것이 부트스트래핑
=:>개념적으로만 보면 원래 표본을 수천 수백만 번 복제하는 것
=>과정
1억개의 모집단에서 200개의 표본 추출
-200개의 표본 중에서 하나를 추출해서 기록하고 복원
-이 작업을 N번 반복
-N번 반복한 데이터를 가지고 통계량을 계산
-이전 과정을 여러 번 반복해서 통계량을 구하고 이 통계량을 이용해서 신뢰구간을 구하는 방식
=>시간이 오래 걸림
=>coffee_dataset.csv 파일의 데이터
-21살 미만 여부
-커피를 마시는지 여부
-키에 대한 데이터
'Study > Data전처리 및 통계' 카테고리의 다른 글
| 추론통계 (0) | 2024.02.27 |
|---|---|
| 추론 통계 (1) | 2024.02.26 |
| 기술 통계 (0) | 2024.02.22 |
| 기초통계 (0) | 2024.02.21 |
| Pandas(8)-한글 NLP (0) | 2024.02.20 |



