1.KNN(K-Nearest Neighbor)

1)개요
=>특징들이 가장 유산한 K개의데이터를 찾아서 K개의 데이터를 가지고 다수결로 클래스를 선택해서 할당
=>회귀에 사용할 떄는 그 값의 평균을 구해서 예측
2)특징
=>간단 - 전처리 과정에서 결측치를 대체하는데 사용하기도 합니다
=>모델을 피팅히는 과정이 없음
=>모든 예측 변수들은 전부 수치형이어야 함
거리를 계산하기 때문
이 경우 범주형 데이터는 특별한 경우가 아니면 원 핫 인코딩을 수행해야 합니다.
=>게으른 알고리즘이라고 하는데 훈련 데이터 세트를 메모리에 전부 저장하고 거리 계산을 수행
온라인 처리가 안됨
=>장점
-이해하기 쉬운 모델
-많이 조정하지 않아도 좋은 성능을 내는 경우가 있음
=>단점
-예측이느림:어떤 알고리즘이 특별히 있는 것도 아니고 예측할 데이터가 오면 그 때가서 이웃을 선정하고 예측함
-많은 특성을 처리하는 능력이 부족: 데이터를 전부 메모리에 로드를 해야하기 때문에 데이터가 많으면 사용하기가 어려움
-게으른 알고리즘
3)API
=>sklearn.neighbors.KNeighborsClassifier 클래스
인스턴스를 생성할 때 n_neighbores 를 이용해서 이웃의 개수를 설정
metric 을 이용해서 거리 계산 알고리즘을 설정하는데 1이면 맨해튼 거리 2이면 유클리드 거리 설정하지 않으면 mincowski 거리
=>데이터는 loan_200.csv
payment_inc_ratio:소득에 따른 대출 상환 비율
dti:소득에 대한 부채 비율
outcpme:상환 여부
=>KNeighborsClassifier 을 이용해서 payment_inc_ration 와 dti에 따른 outcome 분류
#데이터 가졍괴
loan200 = pd.read_csv("C:\\Users\\User\\Desktop\\데이터\\python_machine_learning-main\\python_machine_learning-main\\data\\loan200.csv")
#print(loan200.head())
predictors = ['payment_inc_ratio', 'dti']
outcome = 'outcome'
#테스트 데이터와 예측 변수 및 타겟 벡터 분리
newloan = loan200.loc[0:0, predictors]
X = loan200.loc[1:, predictors]
y = loan200.loc[1:, outcome]
#분류기 생성 - k 의 개수는 20
knn = KNeighborsClassifier(n_neighbors=21)
#훈련
knn.fit(X, y)
#예측
knn.predict(newloan)
print(knn.predict_proba(newloan))
4)거리 지표
=>유클리드 거리
-서로의 차이에 대한 제곱합을 구한 뒤 그 값의 제곱근을 취하는 방식
유클리드 거리를 사용할 떄는 수치형 데이터의 범위를 확인해야 합니다
=>맨해튼 거리
-서로의 차이에 대한 절대값을 구한뒤 모두 더한 거리
=>마할라노비스 거리
-두 변수 간의 상관관계를 사용
-유클리드 거리 나 맨해튼 거리는 상관성을 고려하지 않기 떄문에 상관관계가 있는 feature 들의 거리를 크게 반영
-주성분 간의 유클리드 거리를 의미
-많은 계산이 필요하고 복잡성이 증가하기 때문에 잘 사용하지 않음
-feature들의 상관관계가 높게 나타난다면 마할라노비스 거리 사용하는 것도 고려
=>민코프스키 거리
-1차원 공간에서는 맨하튼 거리를 사용하고 , 2차원 공간에서는 유클리드 거리를 사용
5)표준화(Standardizaion)
=>거리의 개념을 이요하므로 스케링이나 표준화를 수행을 해주어야 합니다.
=>표준화를 했을 떄와 그렇지 않을 때 이웃이 달라지게 됩니다
6)Feature Engineering
=>KNN은 구현이 간단하고 직관적
=>성능은 다른 분류 알고리즘에 비해서 그렇게 우수한 편이 아님
=>다른 분류 방법들의 특정 단계에 사용할 수 있게 모델에 지역적 정보를 추가하기 위해서 사용하는 경우가 많음
-새로운 피처를 만드는게 많이 이용
-기존의 피처를 이용해서 새로운 피처를 만드는 것이라서 다중 공선성( 두 개의 독립변수끼리 강한 상관관계을 가짐)을 야기할 것 같은데 KNN으로 만들어진 피처는 다중 공선성 문제가 거의 발생하지 않음
-KNN은 피처 전체를 이용하는 것이 주위 데이터 몇개만 이용해서 매우 지협적인 정보를 이용
7)loan_data.csv.gz 데이터를 읽어서 새로운 feature을 추가
=>csv 파일의 크기가 너무 커지는 경우 파일을 가지고 다니는데 불편할 수 있는데 이런 경우에는 gz 타입으로 압축을 해서 용량을 줄일 수 있습니다.
pandas 는 gz 로 압축된 csv 파일의 내용을 읽을 수 있습니다.
=>python은 zip 이나 tar 로 압축된 파일을 압축을 해제할 수 있고 여러 파일을 압축할 수 있는 API를 제공합니다.
=>outcome 컬럼을 타겟으로 하고 나머지를 feature 특성을 가지고 타겟을 예측하도록 KNN으로 학습한 후 그 때의 예측확률을 새로운 feature 로 추가
2.나이브 베이즈
1)개요

=>나이브 베이즈 알고리즘은 주어진 결과에 대해 에측 변수 값을 확률을 사용해서 예측 변수가 주어졌을 떄 결과를 확률로 추정
=>완전한 또는 정확한 베이지언 분류 - 나이브 하지 않은 방식:현실성이 떨어지는 방
-예측 변수 프로파일이 동일한 모든 레코드를 찾음
- 해당 레코드가 가장 많이 속한 클래스(타겟)를 결정
- 새로운 레코드에 해당 클래스를 지정
- 모든 예측 변수들이 동일하다면 같은 클래스에 할당될 가능성이 높기 때문에 예측 변수들이 같은 레코드를 찾는데 무게를 두는 방식
- 예측 변수들의 개수가 일정 정도 커지게 되면 분류해야 하는 데이터들이 대부분 완전히 일치하는 경우는 별로 없다.
=>나이브 베이즈
-확률을 계산하기 위해 정확히 일치하는 레코드로만 제한하지 않고 전체 데이터를 활용
2)나이브 베이즈 특징
=>일반적인 선형 분류기 보다 훈련 속도가 빠른 편
=>일반화 성능은 일반적으로 선형 분류기 보다 떨어짐
=>효과적인 이유는 각 특성을 개별로 취급해서 파라미터를 학습하고 각 특성에서 클래스 별 통계를 단순하게 취합: 텍스트 처리에 주로 이용
3)sklearn의 API
=>GaussianNB - 연속적인 데이터 사용
=>BernoulliNB - 이진 데이터 사용
=>MultimonialNB - 카운트 데이터(특성의 개수를 헤아린 정수)
=>BernoulliNB와 MultinomialNB 을 자연어 처리에 이용
4)대출 상환 여부에 나이브 베이즈 분류기 사용
=>나이브 베이즈는 피쳐들의 자료형이 범주형이어야 합니다.
loan_data = pd.read_csv("C:\\Users\\User\\Desktop\\데이터\\python_machine_learning-main\\python_machine_learning-main\\data\\loan_data.csv.gz")
#문자열을 범주형으로 변환
loan_data['outcome'] = pd.Categorical(loan_data['outcome'],
categories =['paid off','default'],
ordered=True)
#purpose_,home_, emp_len은 범주형
#loan_data.info()
#타겟은 순서가 중요함
#분류를 할 때는 각 타겟의 순서대로 확률을 제시
#피처는 순서가 중요하지 않기 떄문에 바로 카테고리로 변환
#나중에 원핫 인코딩도 진행
loan_data['purpose_'] = loan_data['purpose_'].astype("category")
loan_data['home_']= loan_data['home_'].astype("category")
loan_data['emp_len_'] = loan_data['emp_len_'].astype("category")
#타겟과 피처를 분리
predictors = ['purpose_','home_','emp_len_']
outcome = 'outcome'
#get_dummies 를 활용하면 원-핫 인코딩이 자동진행
X=pd.get_dummies(loan_data[predictors],prefix= "",prefix_sep='')
y= loan_data[outcome]
#print(X.head())
from sklearn.naive_bayes import MultinomialNB
#나이브 베이즈 모델 생성 및 훈련
naive_model = MultinomialNB()
naive_model.fit(X,y)
#146번 데이터 예측
new_loan = X.loc[146:146,:]
print("146번 - ",naive_model.predict(new_loan)[0])
print(naive_model.classes_)
#확률을 보면서 cutline
print("146번-",naive_model.predict_proba(new_loan))
Logistic Regression
1)개요
=>타겟이 범주형인 경우 사용하는 회귀 모형
=>분류만 가능
=>타겟이 2가지 값을 갖는 경우에만 사용
=>피처의 자료형이 연속형에도 있고 이산형에도 사용 가능
2)Odds ratio
=>Odds ratio = 성공률/실패율 = 성공율/(1-성공율)
3)Logit 함수
=>Odds Ratio 에 로그를 취한 것
=>자연 로그를 취하게 되면 부드러운 곡선의 형태가 만들어짐
=>직선의 형태로 구분하는 단순 회귀 보다는 조금 더 정확한 모델을 만들 가능성이 높음
경계선 부근에 데이터가 많은 경우
4)API
=>Logistic Regression
- 하이퍼 파라미터:
LogisticRegression(penalty='l2', *, dual=False, tol=0.0001,
C=1.0, fit_intercept=True,
intercept_scaling=1, class_weight=None,
random_state=None, solver='lbfgs',
max_iter=100, multi_class='auto',
verbose=0, warm_start=False,
n_jobs=None, l1_ratio=None)
#penalty:규제
#tol = 중지 기준
#C = 규칙강도의 역수
#n_jobs = 한번에 몇번 실행하는지
Odds = 성공율 /실패율
Odds ratio = 한그룹의 Odds / 다른 그룹의 Odds

5)붓꽃 데이터의 품동을 로지스틱 회귀로 수행
from sklearn import datasets
iris = datasets.load_iris()
X=iris.data
y=iris.target
print(X[:5])
print(y[:5])
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(random_state=42)
log_reg.fit(X,y)
print(X[0].reshape(4,-1))
print(log_reg.predict(X[0].reshape(-1,4)))
print(y[0])
6) softmax 회귀

=> 이진 분류 알고리즘을 가지고 다중 클래스 분류를 할 떄는 여러개의 분류기를 만들어서 처리
클래스 개수 만큼 이진 분류기를 만들어서 분류기를 통과한 결과 중 가장 높은 확률을 가진 클래스로 판정하는 방식과 2개씩 쌍으로 분류할 수 있는 모든 분류기를 만들어서 판정하는 방식
=>여러 개의 이진 분류기를 훈련시켜 연결하지 않고 직접 다중 클래스를 지원하도록 일반화한 방식을 소프트 맥스 회귀라고 합니다.
softmax 함수는 정규화된 지수함수라고도 하는데 각 feature들을 가지고 클래스에 대한 점수를 계산하는 선형회귀 식을 만들어서 사용
각 클래스에 대한 선형 회귀식을 별도로 만들어 두고 회귀 식에 의해서 샘플에 대한 점수가 계산이 되면 softmax 함수를 통과시켜서 확률을 추정
7)Cross-Entropy
=>정보 이론에서 유래
=>여러 개의 상태가 있을 떄 이 상태를 표현하는 방법을 비트 수를 다르게 해서 표현하는 방식
=>자주 등장하는 상태는 비트 수를 적게해서 만들고 자주 등장하지 않는 상태는 비트 수를 크게 만드는 것
현재 상태가 4가지
-일련번호 방식으로 표현
00
01
10
11
-원핫인코딩
1000
0100
0010
0001
-크로스 엔트로피
0 - 첫번쨰 상태
10- 두번째 상태
110- 세번째 상태
1111- 네번째 상태
비트의 값을 확인하는 것이 아닌 비트의 길이로 파악이 가능
8)로지스틱 회귀에서 softmax 사용법
=>multi_class 옵션에 multinomial 을 적용하고 solver 옵션에 lbfgs 같은 softmax 알고리즘을 적용할 수 있는 알고리즘을 선택해야 합니다.
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(multi_class='multinomial',solver='lbfgs',random_state=42)
log_reg.fit(X,y)
print(X[0].reshape(4,-1))
print(log_reg.predict(X[0].reshape(-1,4)))
print(y[0])
4.SVM(Support Vector Machine)
1)개요
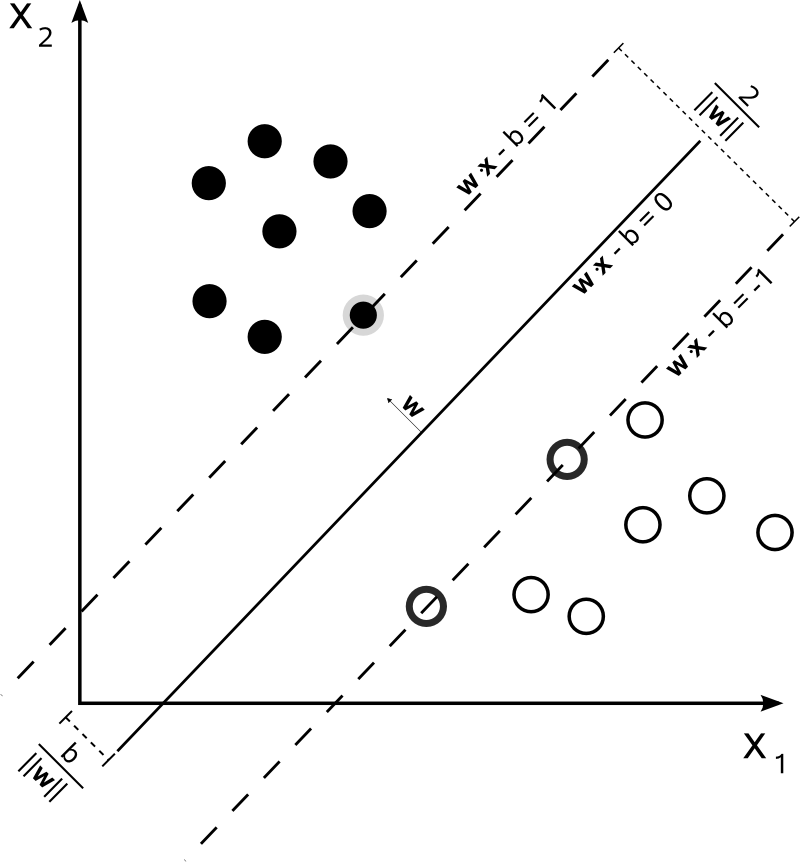
=>일반적인 머신러닝 기법 중에서 매우 강력하고 선형 또는 비선형, 이상치 탐색에도 사용하는 머신러닝 모델
=>초창기에는 가장 인기있는 모델에 속함
=>복잡한 분류 문제에 적합했고 , 작거나 중간 크기의 데이터 세트에 적합
=>모든 속성을 활용하는 전역적 분류 모형
=>군집 별로 초평면을 만드는데 이 초평면은 다른 초평면의 가장 가까운 자료까지의 거리가 가장 크게 만드는 것
2)특징
=>장점
-에러율이 낮음
-결과를 해석하기 용이
=>단점
-파라미터 및 커널 선택에 민감
-이진 분류만 가능
-특성의 스케일에 민감해서 반드시 스케일링을 수행해야 합니다
3)Hard Margin & Soft Margin

=>하드 마진
- 모든 데이터가 정확하게 올바르게 분류된 것
-하드 마진을 성립하려면 데이터가 선형적으로 구분될 수 있어야 하고 이상치에 민감
=>소프트 마진
-이상치로 인해 발생하는 문제를 피하기 위해서 좀 더 유연한 모델을 생성
-어느 정도의 오류를 감안하고 결정 경계를 만들어내는 방식
-SVM에서는 C라는 매개변수로 마진 오류를 설정할 수 있음
-마진 오류는 적은 것이 좋지만 너무 적게 설정하면 일반화(지금껏 보지 못한 데이터에 올바르게 적용되는 성질)이 잘 안됨
4)선형 SVM을 이용하는 붓꽃 분류
=>pipeline 사용
- feature scaling 과 모델 훈련을 하나의 파이프라인으로 묶어서 수행
iris = datasets.load_iris()
X = iris['data'][:,(2,3)] #꽃잎 길이, 꽃잎 너비
y = (iris['target']==2).astype(np.float64)
#이진 분류를 수행하기 위해 타겟을 2인지 아닌지로 생성
#SVM은 feature scaling을 수행
#feature scaling
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
from sklearn.svm import LinearSVC
#모델 생성
svc_clf = LinearSVC(C=1,random_state=42)
svc_clf.fit(X,y)
svc_clf.predict([[5.5,1.7]])
- 모든 컬럼에 동일하게 수행한다면 pipeline으로 묶을 수 있습니다
iris = datasets.load_iris()
X = iris['data'][:,(2,3)] #꽃잎 길이, 꽃잎 너비
y = (iris['target']==2).astype(np.float64)
#이진 분류를 수행하기 위해 타겟을 2인지 아닌지로 생성
#SVM은 feature scaling을 수행
#feature scaling
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
#scaler 와 분류기를 하나로 묶어서 사용
svm_clf = Pipeline([
("scaler",StandardScaler()),
("linear_SVC",LinearSVC(C=1,random_state=42))
])
svm_clf.fit(X,y)
svc_clf.predict([[5.5,1.7]])
5)비선형 SVM
=>개요
-선형 SVM 분류기가 효율적이기는 하지만 선형적으로 분류할 수 없는 데이터가 많음
-선형 SVM(커널)의 문제점 중 하나가 XOR 을 구분할 수 없는 것
-이를 해결하는 방법 중 하나가 다항식을 이용하는 것
XOR을 해결하기 위해서는 선을 2개 이상 만들거나 비선형으로 만들면 됨
=>다항식을 이용하는 SVM을 생성하기 위해서는 PolynomialFeatures 변환기를 추가하면 됩니다
# 데이터 생성
from sklearn.datasets import make_moons
X,y =make_moons(n_samples =100, noise =0.14, random_state=42)
#위의 데이터 시각화
def plot_dataset(X,y,axes):
plt.plot(X[:,0][y==0],X[:,1][y==0],'bs')
plt.plot(X[:,0][y==1],X[:,1][y==1],'g^')
plt.axis=(axes)
plt.grid(True,which='both')
plt.xlabel("x_1",fontsize=20)
plt.ylabel("x_2",fontsize= 20, rotation=0)
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show()
#다항식을 추가한 선형 분류기
from sklearn.preprocessing import PolynomialFeatures
#PolynomialFeatures 의 degree 는 추가되는 다항의 자수승을 의미
#숫자가 높아지면 잘 분류할 가능성이 높아지지만 학습할 피처의 개수가 늘어나고
#이로 이해 학습 속도가 느려질 것이소
#overfitting이 될 가능성이 높아집니다
polynomial_svm_clf = Pipeline([
('poly_features',PolynomialFeatures(degree=3)),
("scaler",StandardScaler()),
("svm_clf",LinearSVC(C=1,random_state=42))
])
polynomial_svm_clf.fit(X,y)
def plot_predictions(clf, axes):
x0s = np.linspace(axes[0], axes[1], 100)
x1s = np.linspace(axes[2], axes[3], 100)
x0, x1 = np.meshgrid(x0s, x1s)
X = np.c_[x0.ravel(), x1.ravel()]
y_pred = clf.predict(X).reshape(x0.shape)
y_decision = clf.decision_function(X).reshape(x0.shape)
plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2)
plt.contourf(x0, x1, y_decision, cmap=plt.cm.brg, alpha=0.1)
plot_predictions(polynomial_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show()
6)다항식 커널
=>다항식 특성을 추가하면 성능이 좋아졌는데 낮은 차수의 다항식은 매우 복잡한 데이터 세트에는 잘 맞지 않을 것이고, 높은 차수의 다항식은 굉장히 많은 특성을 추가하므로 모델을 느리게 함
=>Kernel Trick 이라는 수학적 기교를 이용해서 실제로는 특성을 추가하지 않으면서 다항식 특성을 추가 한것과 같은 효과를 얻을 수 있는 방법을 사용할 수 있음
=>이 기법을 사용할 때는 SVC 클래스를 이용하고 kernel 이라는 매개변수에 poly를 설정하고 degree 라는 매개변수을 적용하고자 하는 차수를 설정하고 coef()라는 매개변수에 정수 값을 설정하는데 낮은 차수와 높은 차수 중에서 어떤 다항식을 영향을 받을지를 설정
#다항식 커널은 실제로 다항식을 추가하는 것이 아니고 추가하는 것과 같은 효과를 냄
from sklearn.svm import SVC
poly_kernel_svm_clf = Pipeline([
("scaler",StandardScaler()),
("svm_clf",SVC(kernel='poly',degree=10,coef0=1,C=1,random_state=42))
])
poly_kernel_svm_clf.fit(X,y)
plot_predictions(poly_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show()
7)유사도 특성을 추가하는 가우시안 RBF 커널
=>몇 개의 랜드마크를 추가한 후 이 랜드마크와 유사도 측정해서 그 값을 특성으로 추가
=>SVC로 생성하고 kernel 에 rbf를 설정하고 gamma를 설정하는데 너무 적은 수 로 설정하면 선형 분류에 가까워지고 높게 설정하면 다항식을 이용하는 분류에 가까워집니다.
#가우시안 rbf 커널은 gamma 를 이용해서 복잡도를 설정
from sklearn.svm import SVC
poly_kernel_svm_clf = Pipeline([
("scaler",StandardScaler()),
("svm_clf",SVC(kernel='rbf',gamma=10,C=1,random_state=42))
])
poly_kernel_svm_clf.fit(X,y)
plot_predictions(poly_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show()8)커널의 종류로 sigmoid도 존재
9)시간 복잡도
문자를 이용해서 행렬을 표현할 때 앞의 숫자가 행의 수이고 뒤의 숫자가 열의 수
-SGDClassifier(선형회귀분류):O(m*n)
-LinearSVC:O(m*n) - 외부 메모리 학습을 지원 => 데이터가 파일에 있어도 괜찮
-SVC:O(m^2 *n) ~ O(m^3* n)
5.Decision Tree(결정 트리)
1) 개요
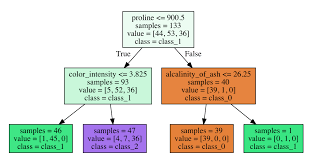
=>데이터를 분석해서 이들 사이에 존재하는 패턴을 예측 가능한 트리 모양의 조건문 형태로 만드는 방식
=>복잡한 데이터 세트도 학습할 수 있는 강력한 알고리즘
=>RandomForest 모델의 기본 구성 요소
=>범주나 연속형 모두 예측 가능하기 때문에 분류와 회귀에 모두 사용할 수 있고 다중출력도 가능한 알고리즘
=>분류에서는 마지막 터미널 값을 그대로 리턴하고 회귀의 경우는 평균을 리턴
=>트리는 한 번 분기할 때마다 변수 영역을 2개로 구분
=>한 번 구분을 한 뒤 순도가 증가하거나 불순도가 감소하는 방향으로 학습을 수행
=> 순도가 증가하거나 불순도가 감소하는걸 정보 획득이라고 합니다
=>API는 DecisionTreeClassifier 이고 max_depth 라는 매개변수를 설정합니다.
max_depth은 트리의 깊이입니다.
2) 트리 시각화를 위한 준비
=>Mac
brew install graphviz
sudo chown -R$계정 /usr/local/share/man/man5
=>Windows
https://graphviz.org/download/#windows 에서 다운로드 받아서 설치
환경변수 중 path 에 설치 디렉토리의 bin 디렉토리와 bin에 있는 dot.exe 경로를 추가
3)트리 시각화
1]트리 모델의 강점
=> 이해가 쉽다 - White Box
트리 구조를 시각화
=>피처의 중요도 파악이 쉽다
=>별도의 파라미터 튜닝을 하지 않아도 좋은 성능
=> 데이터 전처리가 거의 필요 없음
-Scaling 을 할 필요가 없음
iris =datasets.load_iris()
X = iris.data[:,2:]
y= iris.target
from sklearn.tree import DecisionTreeClassifier
tree_clf = DecisionTreeClassifier(max_depth =2,random_state=42)
tree_clf.fit(X,y)
#시각화 부분
from sklearn.tree import export_graphviz
import graphviz
export_graphviz(
tree_clf,
out_file="iris_tree.dot",
feature_names=iris.feature_names[2:],
class_names=iris.target_names,
rounded=True,
filled=True
)
with open('iris_tree.dot') as f:
dot_graph = f.read()
src = graphviz.Source(dot_graph)
src
4)불순도 지표
=>트리 모델은 순도가 증가하는 또는 불순도가 감소하는 방향으로 학습
=>지니 계수(gini index):오분류 오차
1에서 전체 데이터개수에서 분류된 클래스의 데이터 개수를 제곱한 값을 전부 뺀 값
작을수록 좋은 값
ex.) 총 54개의 데이터를 분류 했는데
클래스 1이 0개, 클래스 2가 49개 , 클래스 3이 5개로 분류된 경우
1-(0/54)^2-(49/54)^2-(5/54)^2
=>엔트로피
- 기본적으로는 지니계수를 사용하지만, criterion 을 entropy 로 설정하면 불순도 지표가 변경됨
- 하나의 영역에 2가지 클래스가 배정된 경우
ex.)하나의 영역에 16개의 데이터가 배정되었는데 1번이 10개, 2번이 6개가 배정된 경우의 엔트로피 계산
10/16 * log(10/16) - 6/16*log(6/16)
한쪽으로만 데이터가 배정이 되면 앞의 값이 0 이고 뒤의 값도 0이 되서 0이 됩니다.
만약에 한쪽으로 다 배정이 된게 아니라면 숫자가 나옴.
0에 가까운 값이 좋은 값입니다.
5)규제 매개변수
=>개요
- 결정 트리는 훈련 데이터에 대한 제약 사향 거의 없음
-규제를 하지 않으면 트리가 훈련 데이터가 아주 가깝게 맞출려고 해서 과대 적합이 발생
- 결정 트리는 모델의 하이퍼 파라미터가 없는 것이 아니라 훈련되기 전에 파라미터 수가 결정되지 않기 때문에 모델 구조가 데이터에 맞춰져서 고정되지 않고 자유로움
하이퍼 파라미터의 기본값이 대부분 Max값이거나 None 입니다.
이 전의 다른 모델은 하이퍼 파라미터 값이 설정되어 있습니다.
하이퍼 파라미터의 값이 기본값을 가지는 경우는 과대 적합될 가능성은 낮지만 과소적합될 가능성이 있고, 하이퍼 파라미터의 값이 기본값을 가지지 않고 MAX 값을 가지는 경우 과대적합될 가능성은 높지만 과소 적합될 가능성은 낮습니다
비선형 커널에서 degree 라는 하이퍼 파라미터가 있었습니다. degree 가 높으면 데이터가 정확하게 분류할 확률이 높습니다.
degree을 -1 로 설정할 수 있다고 하면 정확하게 분류할 가능성은 높아지지만, 시간이 너무 오래 걸리고 overfitting이 될 가능성이 높음
=> 결정 트리의 형태를 제한하는 매개변수
-max_depth:최대 깊이, 특성의 개수를 확인해서 적절하게 설정
-min_samples_split: 분할을 할 때 가져야하는 데이터의 최소 개수
-min_samples_leaf: 하나의 터미널이 가져야 하는 최소 개수
-min_weight_fraction_leaf:개수가 아니라 비율로 설정
-max_leaf_nodes:터미널의 개수
-max_features:분할에 사용할 특성의 개수
일반적으로는 min으로 시작되는 매개변수를 증가시키거나 max로 시작하는 매개변수로 감소시키면 규제가 커집니다.
- 규제가 커지면 오차가 발생할 확률은 높아집니다.
6)트리 모델의 단점
=>훈련 데이터의 작은 변화에도 매우 민감하다는 것
조건문을 사용하는 방식이라서 하나의 데이터가 추가되었는데 이 데이터가 조건에 맞지 않으면 트리를 처음부터 다시 만들어야 할 수도 있습니다.
=>트리모델을 훈련시켜서 다른 트리 모델 과 비교하고자 할 때는 반드시 random_state을 고정시켜야 합니다.
7)feature 의 중요도 확인
=>트리 모델에는 feature_importances_ 속성이 있어서 feature의 중요도를 확인할 수 있습니다.
#피처의 중요도 확인
print(tree_clf.feature_importances_)
print(iris.feature_names[2:])iris_importances = pd.Series(tree_clf.feature_importances_,
index=iris.feature_names[2:])
sns.barplot(x=iris_importances, y= iris_importances.index)
plt.xlabel('feature importance')
plt.show()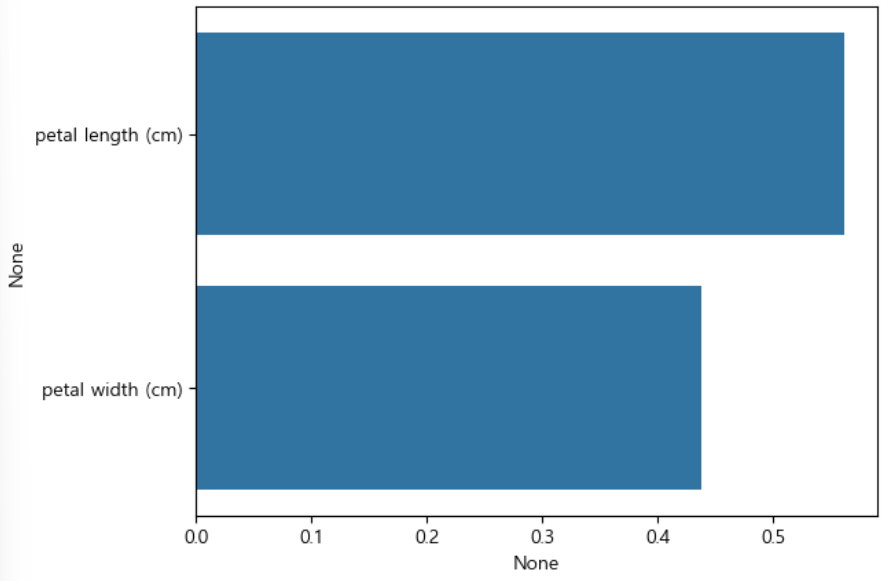
8)최적의 하이퍼파라미터 찾기 - 하이퍼 파라미터 튜닝( max_depth , min_sample_split)
# hyperparamter 튜닝
from sklearn.model_selection import GridSearchCV
#파라미터 모음
parameters ={'max_depth':[1,2,4,6,9,12],
'min_samples_split':[2,4,8,10]}
grid_cv = GridSearchCV(tree_clf,param_grid =parameters,scoring = 'accuracy',cv=5,verbose=1)
grid_cv.fit(X,y)
print("가장 좋은 하이퍼파라미터:", grid_cv.best_params_)
print("가장 좋은 정확도:",grid_cv.best_score_)
'Study > Machine learning,NLP' 카테고리의 다른 글
| 머신러닝(5) - Regression(2) (0) | 2024.03.05 |
|---|---|
| 머신러닝(4)-Regression(1) (0) | 2024.03.04 |
| 머신러닝(2)-Classification(1) (0) | 2024.02.28 |
| 머신러닝(1) (2) | 2024.02.27 |
| 이미지 데이터 다루기 (0) | 2024.02.20 |



