1.회귀
1)개요
=> 두 변수 간의 예측 관계에서 한 변수에 의해서 예측 되는 다른 변수의 예측치들이 그 변수의 평균치로 회귀하는 경향이 있다고 하여 Galton에 의해서 명명
=>한 개의 종속 변수와 독립 변수들 과의 관계를 모델링 한 것으로 종속 변수가 연속형 변수일 때 회귀라 하고 종속 변수가 범주형일 때 분류라고 합니다.
로지스틱 회귀를 제외하고는 거의 모든 모델이 분류와 회귀 양쪽 모두에 사용 가능
결과를 확률로 제시하느냐 아니면 평균으로 제시하느냐 차이
=>분류
회귀를 설명하기 위한 독립 변수의 개수에 따라 단순 회귀(1개) , 다중회귀(2개이상)로 분류
차수에 따라서 선형과 비선형으로 나눔
2.선형 회귀
1)개요
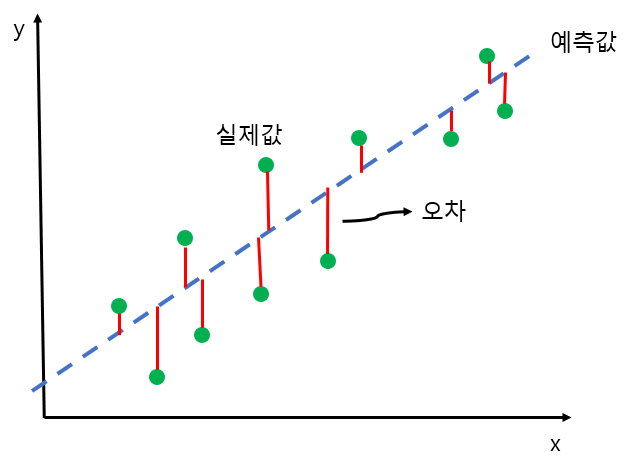
=>실제 값과 예측 값의 차이를 최소화하는 직선형 회귀선을 최적화하는 방식
=>선형 회귀는 규제 방법에 따라 별도의 유형으로 분류하기도 합니다.
규제는 선형 회귀의 overfitting 문제들을 해결하기 위해서 회귀 계수에 패널티를 부여하는 방식 - 회귀 계수를 약화시키거나 제거
2) 단순 선형 회귀
=>독립 변수 (feature)1개와 종속 변수(target) 1개로 이루어진 선형 회귀
=>주택가격이 주택크기로만 결정되는 경우에 이를 하나의 직선으로 표시할 수 있는데 이것이 단순 선형 회귀
(주택가격) = 절편 + 기울기*(주택 크기)
- 이 때 기울기(slope) 와 절편 (interceptor)을 회귀 계수라고 합니다.
-실제 주택 가격은 예측된 주택 가격에 오차를 더하거나 뺀 값
실제 주택 가격과 예측된 주택 가격의 차이를 잔차(residual)라고 합니다.
=>좋은 또는 최적의 회귀 모델을 만든다는 것의 의미는 전체 데이터의 잔차 값이 최소가 되는 모델을 만드는 것 또는 회귀 계수를 찾는 것
3)회귀 모델의 평가 지표
=>MAE(Mean Absolute Error) - 실제 값과 예측 값의 차이를 절대값으로 변환해서 모두 더한 후 평균을 한 것
=>MSE(Mean Squared Error) - 실제 값과 예측 값의 차이를 제곱한 후 모두 더한 후 평균을 한 것
평균 제곱 오차(MSE)는 회귀에서 자주 사용되는 손실 함수. MSE 는 잔차에 제곱을 하기 때문에 MAE 보다는 조금 더 평가 지표로 사용하기 유용하지만 기존 데이터의 스케일이 변경되는 경우가 있어 이를 제곱근한 RMSE를 사용하기도 합니다.
=>MSE 나 RMSE 에 로그를 적용한 MSLE 나 RMSLE 을 사용하기도 합니다.
일반적으로 로그를 사용하는 경우는 데이터가 한쪽에 치우치는 경우 - 이상치, 극단치가 존재하는 경우
종속 변수에 스케일의 범위가 넓고 양 끝단의 데이터가 극단치 형태로 매우 적게 존재하는 경우 로그 스케일을 수행하기도 합니다.
=>R2(Coefficient of Determination- 결정 계수)
1- ((실제 타겟값 - 샘플의 예측값) 을 제곱을 한 합계) /((실제 타겟값 - 타겟 벡터의 평균값)을 제곱을 한 합계)
- 1에 가까울수록 좋은 값
=>sklearn의 철학에서는 score 는 높은 값이 좋은 값인데 잔차는 작을 수록 좋은 값이라서 sklearn 의 score에 평가지표를 적용 할 떄는 앞에 음의 부호를 취하기 위해서 neg_mean_squared_error 의 형태로 설정
결과를 나온 score을 판단할 떄는 음의 부호를 제거하고 판단해야합니다
# 샘플 데이터 생성
from sklearn.datasets import make_regression
#n_informative는 독립 변수중에서 종속 변수와 상관관계를 갖는 수
feature ,target = make_regression(n_samples=100,n_features=3,n_informative=3,
n_targets=1 , noise=50,coef=False,random_state=42)
#선형 모델 생성
from sklearn.linear_model import LinearRegression
ols = LinearRegression()
#교차 검증 수행
from sklearn.model_selection import cross_val_score
print(cross_val_score(ols,feature,target, scoring ='neg_mean_squared_error'))
print(cross_val_score(ols,feature,target, scoring ='r2'))
4)회귀 훈련 방식
=>정규 방정식 이용
- 비용 함수 (잔차의 값을 최소로 하는 함수)를 최소화하는 해석적인 방법이 존재
- 수학 공식을 이용해서 생성이 가능
(피처의 전치 dot 피처) 역행렬 dot 피처의 전치 dot 타겟
-numpy 에서는 행령의 전치는 T 라는 속성이나 transpose 함수를 이용할 수 있고, 역행렬은 numpy.linalg.inv 라는 함수를 이용해서 구현
# 샘플 데이터 생성
X =2 * np.random.rand(100,1)
y= 3 * X+4+np.random.randn(100,1)
#원래 수식은 3 * X + 4 인데 뒤에 잡음을 섞음
#피처 데이터를 앞에 1인 열을 추가해서 2차원 배열로 수정
X_b = np.c_[np.ones((100,1)),X]
print(X_b.shape)
#행렬 연산을 이용해서 정규 방정식을 구현해서 회귀 계수 찾기
result = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
#첫번째 숫자가 절편, 두번쨰 숫자가 기울기
print(result)
from sklearn.preprocessing import add_dummy_feature
theta_best = np.linalg.inv(X_b.T @ X_b) @ X_b.T @ y
X_new = np.array([[0], [2]])
X_new_b = add_dummy_feature(X_new) # add x0 = 1 to each instance
y_predict = X_new_b @ theta_best
y_predict
#sklearn 을 이용한 단순 선형 회귀
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X,y)
lin_reg.intercept_,lin_reg.coef_
-최소 자승법을 이용해서 잔차 제곱을 최소화하는 회귀 계수를 구해주는 API
scipy.linalg.lstsq()
최소 자승법: 어떤 계의 해방식을 근사적으로 구하는 방법, 구하려는 해와 실제 해의 오차의 제곱의 합을 최소화한 해를 구하는 방법
특이값에 차단 비율 (rcond) 을 설정할 수 있습니다.
잔차도 리턴을 해줌
#최소 자승법을 이용한 정규 방정식
theta_best_svd, residuals, rank, s = np.linalg.lstsq(X_b, y, rcond=1e-6)
theta_best_svd
-np.linalg.pinv 라는 APi를 이용해서 구할 수도 있음: 유사 역행렬을 이용
=> 행렬 분해를 이용해서도 구현 가능
- 정규 방정식을 이용하는 방법보다는 효율적
-정규 방정식이나 행렬 분해를 이용하게 되면 예측이 빠름 (predict 속도가 빠름)
computational complexity of nomral equation approach:연산의 복잡도가 O(n^3)에 해당해 입력feature가 많아질수록 연산시간이 커진다. linear regression(SVD)의 complexity는 O(n^2)이므로 normal equation보다 빠름 허나, 두종류 모두 large number featyre일때 안좋음 .특성 수가 2개 증가하면 훈련 속도는 5.3 배에서 8배 정도 증가
=>경사 하강법(Gradient Descent)

-개요
여러 문제에서 최적의 해법을 찾을 수 있는 일반적인 최적화 알고리즘
특성의 수가 많거나 훈련 샘플이 너무 많아서 메모리에 담아 둘 수 없을 떄 적합
비용 함수를 최소화 하기 위해서 parameter를 조정해나가는 방식
parameter vector 를 cost function의 값이 0이 되도록 수정해가는 방식
parameter vector 를 임의값으로 시작(Random Initialize)해서 한 번에 조금씩 비용함수가 감소되는 방향으로 진행해서 알고리즘이 최소값에 수렴할 떄까지 점진적으로 향상 시키는 방식
- 방법
Y = w* X + b를 임의로 생성
평균 제곱 오차(MSE) 가 최소가 되는 w 와 b를 찾는 방식
-학습률 (Learning Rate)
한 번에 학습해나가는 스텝의 크기
학습률이 너무 작으면 알고리즘이 수렴하기 위해서 너무 많은 학습을 해야하고, 너무 크면 최적화되지 않을 수 있음
-배치 경사 하강법(Batch Gradient Descent)
Batch 은 전체 training set 을 의미함. 매 step 에서 전체 훈련 세트 X 에 대해서 비용함수를 계산하는 방식
데이터가 많은 훈련 세트에서는 아주 느림
장점)
전체 데이터에 대해 error gradient 를 계산하기 때문에 optimal 로의 수렴이 안정적으로 진행된다. 전체 데이터에 대해 업데이트가 한번에 이루어지기 때문에 후술할 SGD 보다 업데이트 횟수가 적다. 따라서 전체적인 계산 횟수는 적다.
단점)
한 스텝에 모든 학습 데이터 셋을 사용하므로 학습이 오래 걸린다. local optimal 상태가 되면 빠져나오기 힘듬
-확률적 경사 하강법(Stocastic Gradient Descent)
매 스텝에서 한 개의 샘플을 무작위로 선택하고 그 하나의 샘플에 대한 이용 함수만 계산하는 방식
배치 경사 하강법에 비해서 훈련 속도가 빠른데 훨씬 불안정
비용함수가 매우 불규칙할 때 이용
이 방식은 잘못하면 최적의 결과를 못찾을 수 있기 떄문에 매 스텝에서 학습률을 변경하면서 학습 sklearn의 SGDRegressor 는 기본적으로 이 방식을 이용
장점)
1.Shooting 이 일어나기 때문에 local optimal 에 빠질 리스크가 적다.
2.step 에 걸리는 시간이 짧기 때문에 수렴속도가 상대적으로 빠르다.
단점)
1.global optimal 을 찾지 못 할 가능성이 있다.
2.데이터를 한개씩 처리하기 때문에 GPU의 성능을 전부 활용할 수 없다.
-미니 배치 경사 하강법(Mini- Batch Gradient Descent)
전체 데이터셋에서 뽑은 Mini-batch 안의 데이터 m 개에 대해서 각 데이터에 대한 기울기를 m 개 구한 뒤, 그것의 평균 기울기를 통해 모델을 업데이트 하는 방법
전체 데이터 셋을 여러개의 mini-batch 로 나누어, 한 개의 mini-batch 마다 기울기를 구하고 모델을 업데이트 하는 것
각 스텝에서 임의의 작은 샘플 세트에 대해 gradient를 계산
장점)
1.BGD보다 local optimal 에 빠질 리스크가 적다.
2.SGD보다 병렬처리에 유리하다.
3.전체 학습데이터가 아닌 일부분의 학습데이터만 사용하기 때문에 메모리 사용이 BGD 보다 적다.
단점)
1.batch size(mini-batch size) 를 설정해야 한다.
2.에러에 대한 정보를 mini-batch 크기 만큼 축적해서 계산해야 하기 때문에 SGD 보다 메모리 사용이 높다.
-각 알고리즘의 비교

=>sklearn.linear_model.LinearRegression
-예측 값과 실제 값의 RSS( Residual Sum of Squares - 잔차 제곱합)을 최소화한 OLS(Ordinary Least Squares) 추정 방식으로 구현한 클래스
-OLS : 어떤 계의 해방정식을 근사적으로 구하는 방법으로 오차의 제곱합이 최소가 되는 해를 구하는 방법
노이즈에 취약
입력 feature의 독립성에 많은 영향을 받는데 feature 간의 상관관계가 매우 높은 경우 분산이 매우 커져서 오류에 매우 민감한데 이러한 현상을 다중 공선성(Multi -Colinearity) 문제라고함
이러한 경우는 독립적인 중요한 feature 만 남기고 제거하고나 규제를 적용하거나 PCA 등을 통해서 차원축소를 수행
-parameter
fit_intercept : bool 값으로 디폴트는 True로 절편을 계산할 것인지의 여부로 False 로 설정하면 절편이 0
normalize : bool 값으로 default 은 False 인데 True 로 설정하면 회귀를 수행하기 전에 입력 데이터 세트를 정규화
copy_X :feature 의 복제 여부로 기본값은 True
n_jobs: 병렬 처리를 수행할 때 동시게 수행할 개수로 기본값은 1이고 일반적으로 -1 로 설정
-결과
coef : 기울기를 배열 형태로 리턴
intercept: 절편 값
-단변량 선형 회귀의 경우는 scipy의 stats 모듈의 linregress 함수를 이용하기도 함
기울기, 절편, 상관계수, p-value, error의 표준편차가 같이 리턴
=>보스톤 주택 가격 예측
- 데이터 : https://lib.stat.cmu.edu/datasets/boston
- 데이터에 대한 설명
The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic
prices and the demand for clean air', J. Environ. Economics & Management,
vol.5, 81-102, 1978. Used in Belsley, Kuh & Welsch, 'Regression diagnostics
...', Wiley, 1980. N.B. Various transformations are used in the table on
pages 244-261 of the latter.
Variables in order:
CRIM per capita crime rate by town
ZN proportion of residential land zoned for lots over 25,000 sq.ft.
INDUS proportion of non-retail business acres per town
CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
NOX nitric oxides concentration (parts per 10 million)
RM average number of rooms per dwelling
AGE proportion of owner-occupied units built prior to 1940
DIS weighted distances to five Boston employment centres
RAD index of accessibility to radial highways
TAX full-value property-tax rate per $10,000
PTRATIO pupil-teacher ratio by town
B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
LSTAT % lower status of the population
MEDV Median value of owner-occupied homes in $1000's
- MEDV 컬럼이 타겟이고 나머지가 feature
-데이터 읽어오기
data_url = 'http://lib.stat.cmu.edu/datasets/boston' # csv 로 되있으면 이렇게 바로가져올수 잇음
#공백문자 단위로 데이터 분할해서 읽음
#공백문자가 \s이고 +를 추가한 이유는 맨 앞에 공백이 있으면 제거하기 위해서
#뒤의 3개의 데이터도 하나의 행에 포함이 되야 하는데 뒷줄로 넘어감
raw_df = pd.read_csv(data_url,sep='\s+',skiprows=22,header=None)
print(raw_df.head())
데이터 행이 벗어남. hstack을 활용해서 데이터 수
-홀수 행에서 짝수 행의 데이터의 3개의 열을 옆으로 붙이기
#짝수 행의 2개의 열을 홀수 행에 붙이기
#feature 만들기
data = np.hstack([raw_df.values[::2,:],raw_df.values[1::2,:2]])
#타겟 만들기
target=raw_df.values[1::2,2]
print(data)
print(target)
- 데이터 프레임 생성 : feature의 이름을 출력하거나 데이터를 전처리할 때 feature 의 이름을 사용할 수 있어서
bostonDF = pd.DataFrame(data, columns=['CRIM','ZN','INDUS','CHAS','NOX','RM','AGE','DIS','RAD',
'TAX','PTRATIO','B','LSTAT'])
bostonDF['PRICE']=target
bostonDF.info()
-선형 회귀를 사용하기 전에 확인할 작업은 타겟과 feature 의 선형 관계 여부 : 산포도를 이용해서 파악(여러 개의 컬럼 사이의 산포도를 만들 때는 seaborn의 pairplot 나 regplot 이용)
#이 API가 예전에는 숫자가 아닌 컬럼이 있으면 제외하고 출력했는데
#최신 API에서는 숫자 컬럼에 대해서만 동작하는데, 숫자 아닌 컬럼이 있으면 에러가 남
sns.pairplot(bostonDF,height=2.5)
plt.tight_layout()
plt.show()위 방법은 feature 가 많은 경우 불필요한 산포도가 너무 많이 그려져서 알아보기가 어려움. 따라서 다른 방법 선택
# 타겟 과의 관계를 파악하고자 하는 feature 리스트 생성
lm_features = ['CRIM','ZN','INDUS','CHAS','NOX','RM','AGE','DIS','RAD',
'TAX','PTRATIO','B','LSTAT']
#한줄에 4개씩 13개의 그래프 영역을 생성
fig, axe = plt.subplots(figsize=(16,8), ncols=4, nrows=4)
#python 에서 list 를 순회할때 인덱스를 같이 사용하는 방법
for i ,feature in enumerate(lm_features):
row = int(i/4)
col = i % 4
sns.regplot(x=feature,y='PRICE',data=bostonDF, ax=axe[row][col])
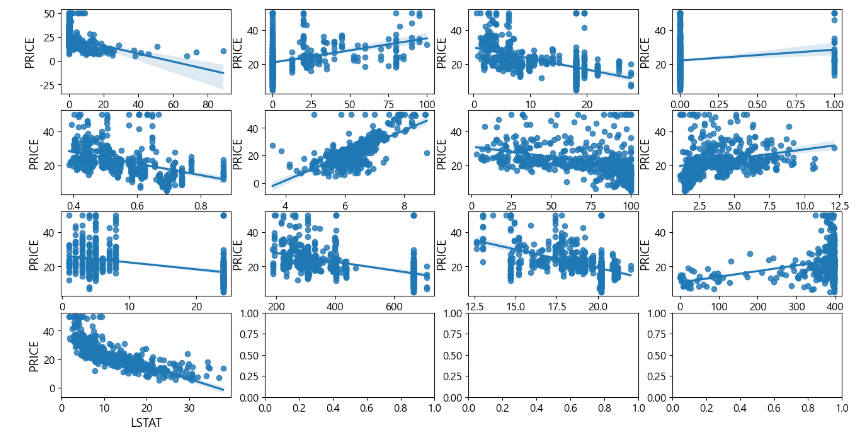
-타겟과 feature 간의 상관관계 확인
# 상관 계수 구하기
cols = lm_features.copy()
cols.append('PRICE')
cm = np.corrcoef(bostonDF[cols].values.T)
#print(cm)
plt.figure(figsize=(15,7))
sns.set(font_scale=1.5)
#ticklabels은 보여질 문자열
#anoot_kws 은 글자 크기
#fmt 은 포맷
#annot는 값 출력 여부
hm=sns.heatmap(cm,cbar=True, annot=True,square=True , fmt='.2f',
annot_kws={'size':12},yticklabels=cols,xticklabels=cols)
plt.show()
-데이터 탐색 결과
RM 과 LSTAT 의 PRICE 의 영향도가 높음
RM은 양의상관관계를 갖고 LSTA 는 음의 상관관계를 가짐
단변량(feature 가 1개) 선형 회귀를 수행한다면 2개의 feature 중 하나를 이용하는 것이 효율적
-scipy 를 이용한 단변량 선형 회귀
from scipy import stats
#scipy는 머신러닝을 수행하지만 머신러닝만을 위한 패키지는 아닙니다
#feature 을 설정할 때 2치원 배열이 아니어도 됩니다.
#scipy 나 seaborn 의 데이터는 pandas의 자료구조가 가능합니다
print(stats.linregress(bostonDF['RM'],bostonDF['PRICE']))
result=stats.linregress(bostonDF['RM'],bostonDF['PRICE'])
#하나의 속성 출력
print(result.pvalue)
-sklearn을 이용한 단변량 선형 회귀
from sklearn.linear_model import LinearRegression
#모델을 생성 - 행렬 분해를 이용하는 선형 회귀 모델
slr =LinearRegression()
#타겟과 feature 생성
#sklearn 에서는 feature가 2차원 배열이어야 합니다
#타겟은 일반적으로 1차원 배열입니다
X=bostonDF[['LSTAT']].values
y=bostonDF['PRICE'].values
#훈련 - 통계 패키지는 훈련의 결과를 리턴합니다
slr.fit(X,y)
print(dir(slr))
#기울기와 절편 출력
print("기울기:",slr.coef_[0])
print("절편:",slr.intercept_)
#예측
print(slr.coef_[0] * 4 + slr.intercept_)
print(slr.predict([[4]]))
=>선형 회귀에서의 이상치 관련 문제
-선형 회귀는 이상치에 민감
-데이터의 작은 일부분이 추정 모델의 가중치에 큰 영향을 미침
-해결책
이상치를 감지해서 제거한 후 수행
이상치를 제거하지 않고 RANSAC(RANdom Sample Consensus) 방식으로 해결
랜덤하게 일부 샘플을 선택해서 모델을 훈련
사용자가 지정한 입력 허용 오차(잔차) 안에 속한 데이터 만을 정상적인데이터로 간주
정상적인 데이터만을 가지고 다시 훈련
훈련된 모델과 정상적인 데이터 와의 오차 추정
사용자가 지정한 임계값에 성능이 도달하거나 반복 횟수에 도달하면 알고리즘을 종료
-API
RANSACRegressor(선형 분류기, max_trials = 최대 반복 횟수, min_samples= 최소 샘플 개수, loss = '평가 지표',
residual_threshold=잔차 임계값, random_state=시드)
5)일반화
=>모델이 처음 보는 데이터에 대해 정확하게 예측할 수 있는 능력
머신러닝의 목적
=>알고리즘이 새로운 데이터도 잘 처리하는지 측정하는 방법은 테스트 세트로 평가해 보는 것
=>일반화가 잘 된 모델은 간단한 모델일 가능성이 높음
=>가진 정보를 모두 사용해서 너무 복잡한 모델을 만드는 것을 과대 적합(Overfitting)이라고 합니다
훈련 데이터에 너무 가깝게 맞춰져서 새로운 데이터에 일반화되기 어려운 상황
=>모델이 너무 간단하면 데이터의 면면과 다양성을 잡아내지 못하게 되고 이러면 훈련 데이터에도 잘 맞지 않을 수 있는데 이런 경우는 과소적합(Underfitting)이라고 합니다
=>MSE 나 결정계수를 이용해서 확인
sklearn.metrics 패키지에 함수 제공
=>이 경우에는 훈련 데이터에서 예측한 것과 테스트 데이터에서 예측한 값을 비교
이차이가 적어야 합니다.
=>훈련 데이터와 테스트 데이터로 나누어서 훈련 한 후 MSE을 비교
X=bostonDF[['RM']].values
y=bostonDF[['PRICE']].values
#훈련데이터와 테스트 데이터 분할
from sklearn.model_selection import train_test_split
X_train, X_test , y_train, y_test = train_test_split(X,y,test_size=0.3,random_state=42)
from sklearn.linear_model import LinearRegression
slr= LinearRegression()
#훈련
slr.fit(X_train,y_train)
#예측
y_train_pred = slr.predict(X_train)
y_test_pred = slr.predict(X_test)
from sklearn.metrics import mean_squared_error,r2_score
#일반적으로 테스트 데이터의 잔차 제곱합이 클 가능성이 높음
#차이가 크면 overfitting일 가능성이 높음
#테스트 데이터가 적게 나오면 underfitting일 가능성이 높음
#과소 적합인 경우는 sample의 개수를 늘리거나 feature의 개수를 늘려야함
print("TRAIN-MSE:",mean_squared_error(y_train,y_train_pred))
print("TEST-MSE:",mean_squared_error(y_test,y_test_pred))
#테스트 데이터가 더 적게 나오는게 일반적
#차이가 적은 모델이 일반화가 잘된 모델
#결정계수(R2 score)은 최소 0.6~0.7 정도는 되어야 사용가능한 모델로 간주합니다
print("Train-R2score:",r2_score(y_train,y_train_pred))
print("Test-R2score:",r2_score(y_test,y_test_pred))
6)다변량 선형 회귀에서의 다중 공선성 문제
=>다변량 선형 회귀: 독립 변수의 개수가 2개 이상인 선형 회귀로 별도의 API는 없고 기존의 선형 회귀 API애서 feature만 변경해주면 됩니다.
=>다중 공선성(Multicollinearity)
- 독립 변수들 간의 강한 상관관계가 나타나는 문제
-독립 변수들 간의 정확한 선형 관계가 존재하는 완전 공선성의 경우와 높은 선형 관계가 존재하는 다중 공선성으로 구분하기도 함
-회귀 분석의 전제 가정을 위배하는 것
회귀 분석의 전제 가정 중 하나는 모든 feature들이 서로 독립적이어야한다 입니다
-확인하는 방법
결정 계수의 값은 높은데 독립변수들의 p-value 가 커서 개별 인자들이 유의하지 않은 경우
독립 변수들 간의 상관 계수를 확인
분산 팽창 요인★(VIF -Variance Inflation Factor)를 구하여 이 값이 10이 넘는 경우 다중 공선성의 문제가 있는 것으로 판단
분산 팽창 요인 - 독립변수가 여러개 있을 때, 특정 독립변수를 종속변수로하고 나머지 독립변수를 독립변수로 하여 회귀분석을 수행하여 변수간에 관계성을 측정
- 해결책
상관 관계가 높은 독립 변수 중 하나 또는 일부를 제거
변수를 변형하거나 새로운 관측치를 이용
자료를 수집하는 현장의 상황을 확인해서 상관관계의 이유를 찾아서 해결
PCA(주성분 분석)을 이용해서 diagonal matrix 의 형태로 공선성을 제거
=>다변량 선형 회귀를 수행해주는 statsmodels 패키지를 활용
- ols 라는 함수에 formula 매개변수에 '종속 변수 ~ 독립변수 [+독립변수]',data =데이터프레임).fit()을 호출하면 결과를 리턴
params 에 절편과 각 독립변수의 기울기를 Series로 리턴
pvalue 가 유의 확률
rsquared 가 결정 계수
=>scores.csv 파일을 읽어서 다변량 선형 회귀를 수행
-데이터에는 name ,score, iq, academy, game, tv 컬럼으로 구성
name은 이름이고, score 가 타겟
#데이터 읽어오기
df = pd.read_csv("C:\\Users\\User\\Desktop\\데이터\\python_machine_learning-main\\python_machine_learning-main\\data\score.csv")
df.head()
#다변량 선형 회귀 수행
import statsmodels.formula.api as sm
result = sm.ols(formula ='score~iq + academy+game+tv',data=df).fit()
print("절편과 기울기:",result.params)
print("결정 계수:",result.rsquared)
print("유의 확률:",result.pvalues)
#결정 계수는 0.96 으로 상당히 높고 각 feature 의 유의확률도 높은 편
#유의 확률이 높으면 우연히 그렇게 나올 수 있따는 의미이므로 높으면 무의미
#이 경우가 다중 공선성이 의심되는 경우
# 상관 계수 확인
X=df.drop(['name'],axis=1)
print(X.corr())
iq 와 academy 그리고 tv 사이에 상관계수가 높은 편
# VIF (분산 팽창 요인)확인
from statsmodels.stats.outliers_influence import variance_inflation_factor
vif = pd.DataFrame()
vif['분산 팽창 요인'] = [variance_inflation_factor(X.values,i) for i in range(X.shape[1])]
vif['features'] = X.columns
print(vif)
보면 score, id ,academy가 높게 나오는 편이라서 이를 제거하고 다시확인
# VIF (분산 팽창 요인)확인
#하나의 컬럼을 제거하고 확인
X = df.drop(['name','score','academy'],axis=1)
from statsmodels.stats.outliers_influence import variance_inflation_factor
vif = pd.DataFrame()
vif['분산 팽창 요인'] = [variance_inflation_factor(X.values,i) for i in range(X.shape[1])]
vif['features'] = X.columns
print(vif)
#다변량 선형 회귀 수행
import statsmodels.formula.api as sm
result = sm.ols(formula ='score~iq+game+tv',data=df).fit()
print("절편과 기울기:",result.params)
print("결정 계수:",result.rsquared)
print("유의 확률:",result.pvalues)
#이전에 비해서 결정계수의 값은 조금 나빠졌지만 유의 확률은 많이 감소했습니다
7) 다항 회귀
=>개요
- 회귀 계수가 독립 변수의 단항식이 아닌 다항식인 경우
- 비선형 회귀는 회귀 계수가 비선형인 경우
독립 변수의 선형 과 비선형 여부와는 아무런 관계가 없음
-실세계에 존재하는 대다수의 데이터는 단순 선형 회귀 직선형으로 표현한 것 보다 다항회귀 곡선형으로 표현한 것이 예측 성능이 높음
=>sklearn에서는 다항 회귀를 위한 클래스를 제공하지 않기 떄문에 비선형 함수를 선형 모델에 적용시키는 방법을 사용
=>sklearn에서는 PolynomialFeatures 클래스를 이용해서 다항식 feature 로 변환시킬 수 있음
degree 에 원하는 다항값을 설정하면 됩니다
from sklearn.preprocessing import PolynomialFeatures
X=np.arange(4).reshape(2,2)
print(X)
#2차 다항 feature 를 생성
poly = PolynomialFeatures(degree=2)
result = poly.fit_transform(X)
#첫번째 데이터는 무조건 1, 두번째 와 세번째 데이터는 그대로
#네번째 와 여섯번째 데이터는 제곱한 값이고 다섯번째 데이터는 곱한 값
print(result)
=>다항 회귀 적용
-샘플 데이터를 추가해서 생성
m =100
X=6 * np.random.rand(m,1)-3
#0.5 * X의 제곱 + X + 2+ 잡음
y=0.5 * X **2 + X + 2+ np.random.randn(m,1)
# extra code – this cell generates and saves Figure 4–12
plt.plot(X, y, "b.")
plt.xlabel("$x_1$")
plt.ylabel("$y$", rotation=0)
plt.axis([-3, 3, 0, 10])
plt.show()
- 일반적인 선형 회귀 적용
#선형 회귀 적용
lin_reg = LinearRegression()
lin_reg.fit(X,y)
print(lin_reg.intercept_,lin_reg.coef_)
#예측해서 시각화
X_new = np.linspace(-3,3,100).reshape(100,1)
y_new =lin_reg.predict(X_new)
plt.plot(X,y,'b.')
plt.plot(X_new,y_new,'r-',linewidth=2)
plt.axis([-3, 3, 0, 10])
plt.show()
-다항 회귀 적용
#다항식을 추가한 데이터 생성
poly_features = PolynomialFeatures(degree=2,include_bias=False)
X_poly = poly_features.fit_transform(X)
#선형 회귀를 수행
#알아서 다항식의 형태로 만들어줍니다
#sklearn의 선형회귀는 다항의 특성도 자동으로 학습합니다
lin_reg = LinearRegression()
lin_reg.fit(X_poly,y)
print(lin_reg.intercept_,lin_reg.coef_)
X_new = np.linspace(-3, 3, 100).reshape(100, 1)
X_new_poly = poly_features.transform(X_new)
y_new = lin_reg.predict(X_new_poly)
plt.figure(figsize=(6, 4))
plt.plot(X, y, "b.")
plt.plot(X_new, y_new, "r-", linewidth=2, label="Predictions")
plt.xlabel("$x_1$")
plt.ylabel("$y$", rotation=0)
plt.legend(loc="upper left")
plt.axis([-3, 3, 0, 10])
plt.show()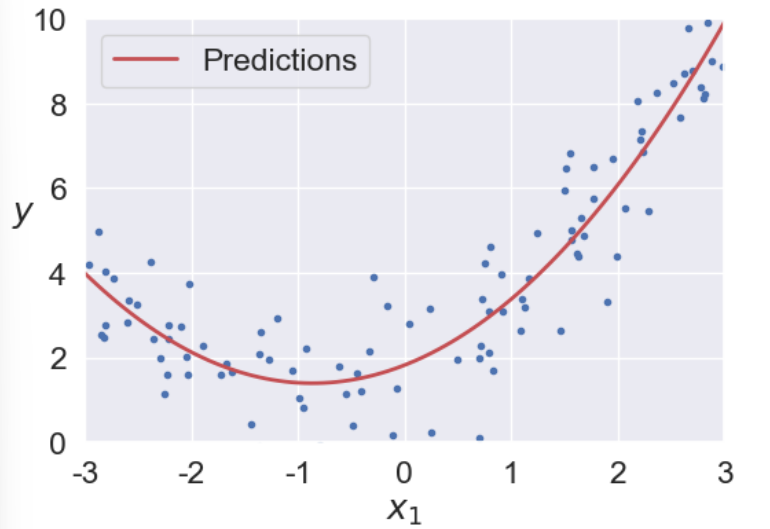
차수를 늘리면 잔차를 거의 없앨 수 있지만 무작정 늘리는 것은 훈련시간을 느리게 하고 과대적합의 문제가 생길 수 있습니다. 아래 그림과 같이 훈련 데이터에 대해서는 거의 완벽하게 맞추지만, 새로운 데이터가 들어왔을 때 해결할 수 있습니다.
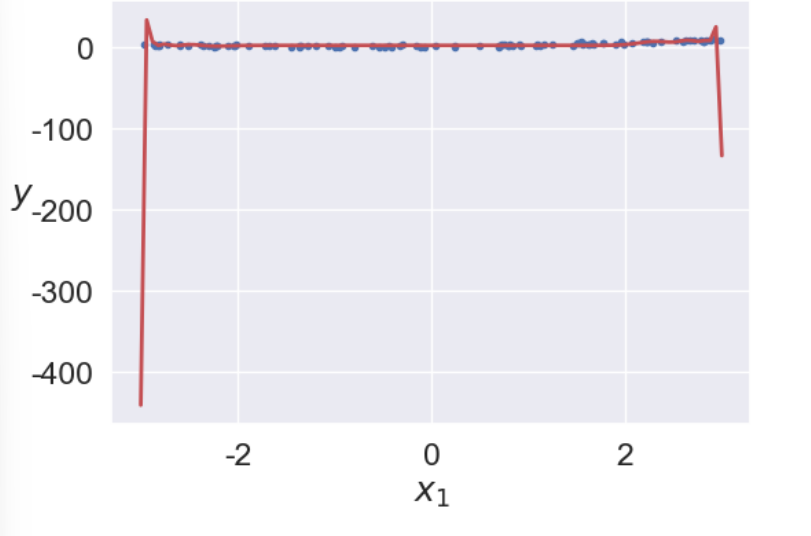
8)편향 /분산 트레이드오프(Bias - Variance TradeOff)
=>모델의 일반화 ( 새로운 데이터를 정확히 예측하는 능력) 오차 종류
-편향
잘못된 가정으로 인해서 발생하는 것
데이터가 실제로는 2차인데 선형으로 가정해서 과소적합되는 형태
-분산
훈련데이터에 있는 작은 변동에 모델이 과도하게 민감하게 반응하면서 나타나는 것으로 자유도가 높은 모델(고차 다항 회귀 모델)이 높은 분산을 가지기 쉬운데 분산이 커지면 과대 적합
- 줄일 수 없는 오차
데이터 자체에 있는 잡음 떄문에 발생
이 오차는 모델을 가지고 제거할 수는 없고 데이터 소스를 수정하거나 이상치를 감지해서 제거하는 방법을 이용
=>모델의 일반화 오차는 세가지 오차의 합으로 표현
=>모델의 복잡도가 커지면 분산이 늘어나고 편향이 줄어들고 반대로 모델의 복잡도가 줄어들면 편향이 커지고 분산이 작아지게 됩니다.
이를 분산/편향 트레이드 오프라고 합니다
9)규제
=>과대 적합을 줄이는 방법 중 하나로 자유도를 줄이는 방법이 있는데 다항식의 차수를 줄이면 됩니다.
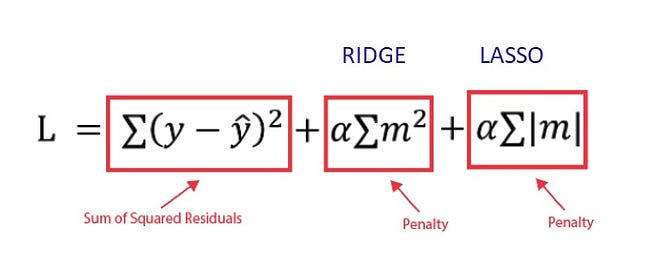
=>Loss
-L1 loss : 실제 값과 예측치 사이의 오차의 절대값을 구한 후 전체를 더한 것이 L1 loss
편차가 다른 경우 값이 다르게 나오지 않을 수도 있습니다
-L2 loss: 오차 제곱 합
L2 loss 가 이상치에 영향을 크게 받음
-Outlier가 적당히 무시되기를 원하면 L1 Loss 를 사용하면 되고 Outlier 의 등장에 신경을 써야 하면 L2 loss 를 사용하는 것을 권장
=>일반화 시키는 방법
- 공선성을 다루거나 잡음을 제거해서 과대 적합을 방지
- 모델 복잡도에 패널티를 주는 방법:규제(영향력이 적은 feature을 제거하거나 영향력을 감소)
Ridge:L2 정규화
Lasso:L1 정규화
ElasticNet: L1 정규화 + L2 정규화의 조합
=>Ridge
-L2 정규화라고 함
-잔차 제곱합 + 패널티 항(베타값)의 합으로 회귀식을 만들어서 미분이 가능해서 경사 하강법이 최적화할 수 있도록 해주고 파라미터의 크기를 작은 것보다 큰 것을 더 빠른 속도로 줄여주는 방식
-패널티를 이용해서 분산을 줄이고 편향을 늘리는 방향으로 동작
-SGDRegressor 클래스의 인스턴스를 만들 떄 penalty 를 L2 로 설정하고 alpha로 베타 값을 설정하면 됩니다
Ridge 라는 클래스를 이용해서도 구현 가능
-alpha 값을 크게 하면 일반적으로 오차가 줄어듭니

np.random.seed(42)
m=20 #데이터 개수
X= 3 * np.random.rand(20,1)
y=1+ 0.5 * X + np.random.randn(m,1)/1.5
from sklearn.linear_model import SGDRegressor
#확률적 경사 하강법을 이용한 구현
#max_iter는 최대 반복 횟수
#eta0은 학습률
sgd_reg = SGDRegressor(penalty ="l2",alpha=0.1/m,max_iter=1000,eta0=0.01,random_state=42)
sgd_reg.fit(X,y)
sgd_reg.predict([[1.5]])
=>Lasso
-L1 정규화라고 함
-잔차의 절대값을 더해서 규제를 가하는 방식
-절대값은 0에 가까울 떄 미분을 할 수 없음
-몇몇 특성을 선택하는 효과 - 유의미하지 않은 변수들의 계수를 0ㅇ으로 만들어버리기도 합니다.
-덜 중요한 feature 들의 회귀계수가 0이 되는 것을 확인할 수 었습니다

=>ElasticNet
-릿지와 라쏘의 혼합 모델
-규제 항은 릿지와 회귀의 규제 항을 단순히 더해서 사용하면 혼합 정도는 혼합 비율 r을 사용해서 조절
-r의 값이 0이면 릿지 회귀가 되고 1이면 라쏘 회귀가 됩니다.
-보통의 경우 선형 회귀는 규제가 있는 것이 대부분의 경우 좋은 성능을 나타내는데 기본적으로 릿지를 사용하고 특성이 몇 개만 적용 되는 것으로 의심되면 라소나 엘라스틱 넷이 조금 더 나은 성능을 발휘
라쏘는 공선성을 확인하지 않게 되면 문제를 일으키는 경우가 있기 때문에 엘라스틱넷을 선호
-sklearn에서는 alpha을 적용하고 l1_ratio 에 l1 정규화 비율을 설정해서 수행
from sklearn.linear_model import ElasticNet
sgd_reg =ElasticNet(alpha=alpha,random_state=42)
sgd_reg.fit(X,y)
print(sgd_reg.predict([[1.5]]))
10) 조기종료

=>경사 하강법 과 같은 반복적인 학습 알고리즘을 규제하는 다른 방식은 검증 에러가 최소값에 도달하면 훈련을 중지시키는 것으로 조기종료라고 합니다.
=>훈련을 할 때 에러는 줄어드는 것이 일반적이지만 교차 검증을 수행할 때 에러가 일시적으로 멈췄다가 다시 상승하는 경우가 있는데 이 경우 훈련 데이터가 과대적합되는 시점입니다.
=>조기 종료는 검증 에러가 최소에 도달하는 즉시 훈련을 멈추는 것
=>이 경우는 반드시 훈련 데이터와 검증하기 위한 데이터를 나누어서 수행을 해야 합니다.
11)선형 회귀에서의 데이터 변환
=> 선형 회귀 모델은 feature 와 target 사이에 선형관계가 있다고 가정하고 최적의 선형 함수를 찾아서 결과를 예측하는 방식인데 가장 좋은 성능을 발휘하는 경우는 정규 분포에 가까운 형태인 경우입니다.
특정 값의 분포가 한쪽에 치우친 왜곡된 분포일 경우 예측 성능에 부정적인 영향을 미칠 가능성이 높음
=>feature 을 scaling하거나 정규화 작업을 수행해서 사용하는데 스케일링하거나 정규화 작업을 수행한 경우가 반드시 성능이 좋지만은 않기 때문에 중요 feature 들이나 타겟 값들의 분포가 심하게 왜곡된 경우에만 변환 작업을 수행
=>sklearn을 이용해 feature 데이터 세트에 적용하는 변환 작업
-StandardScaler (평균이 0 분산이 1인 표준 정규 분포를 가진 데이터세트로 변환) 와 MinMaxScaler (최소값이 0 최대값이 1인 분포)
-앞에서 수행한 Scale 된 데이터에 다항 특성을 추가
-log 함수를 적용하는 log 변환 : 일반적으로 선형회귀는 분포에 영향을 많이 받기 때문에 첫번째 방법으로는 성능 향상을 가져오는 경우가 거의 없으며 두번째 방법이 조금 더 유용하기는 한데 feature가 많은 경우 feature의 수가 기하급수적으로 늘어나서 과대적합이 발생할 가능성이 있어서 로그변환을 많이 시도
=>타겟은 거의 대부분 로그 변환을 수행
정규 분포로 변환을 하면 원래의 값을 찾을 수 있기 때문
=>일반 log 함수를 이용하게 되면 언더플로우가 발생할 수 있기 때문에 log함수를 적용한 후 1을 더해서 언더플로우를 방지하는데 이에 사용하는 함수가 np.log1p()
'Study > Machine learning,NLP' 카테고리의 다른 글
| 머신러닝(6)-Ensemble (0) | 2024.03.05 |
|---|---|
| 머신러닝(5) - Regression(2) (0) | 2024.03.05 |
| 머신러닝(3)-Classification(2) (0) | 2024.02.29 |
| 머신러닝(2)-Classification(1) (0) | 2024.02.28 |
| 머신러닝(1) (2) | 2024.02.27 |



