2.비선형 회귀
1)개요
=>회귀 계수의 결합이 비선형인 경우
=>회귀 함수를 기반으로 하지 않음
2)KNN(K-Nearest Neighbors)회귀
=>새로운 데이터가 들어온 경우 가장 가까운 이웃 몇 개를 찾아서 그 이웃의 데이터를 가지고 분류의 경우는 투표를 해서 다수결로 타겟을 결정하고 회귀의 경우는 평균을 이용해서 타겟을 결정하는 방식
=>가중회귀
-일반적인 경우
현재 위치에서 거리가 가장 가까운 3개를 추출
A 거리가 3.2인데 5
B 거리가 11.5인데 6.8
C 거리가 1.1 인데 9.0
(5+6.8+9.0)/3 :6.9 정도
-거리에 따라서 가중치를 부여하는 방식
(5/3.2 + 6.8/11.5 + 9.0/1.1) /(1/3.2 +1/11.5 +1/1.1)으로 계산
-KNN을 생성할 때 weights 매개변수에 distance 를 설정하면 거리에 따른 가중치를 적용할 수 있습니다.
=>KNN은 게으른 알고리즘: 데이터를 예측하기 위해서 모든 데이터가 메모리에 상주해야하는 알고리즘
=>이해하기 쉬운 White-Box 알고리즘 이고 별도의 훈련을 거치지 않은 쉬운 알고리즘이라서 데이터 전처리(결측치 대체나 새로운 피쳐 추가 - 지역적 정보를 이용하기 때문에 다중 공선성 문제는 고려할 필요가 없음)에 많이 이용합니다.
=>API는 sklearn.neigbors.KNeighborsRegressor
from sklearn.neighbors import KNeighborsRegressor
#가중 평균 적용
regressor = KNeighborsRegressor(n_neighbors=3,weights='distance')
regressor.fit(X_data,X_target)
print(X_data.head())
#print(X_data.loc[0].values.shape(13,1))
print(regressor.predict(X_data.loc[0].values.reshape(1,13)))
print(X_target.loc[0])
3)Decision Tree
=>개요
-트리 기반으로 리프에 도달하면 리프 데이터의 평균을 가지고 예측
-불순도 지표
지니 계수(오분류 오차): 1 - (예측한 개수/전체 개수)^2-(예측한 개수/전체 개수)^2 ...
한쪽으로만 분류가 되면 0: 가장 좋은 형태
가장 나쁜값이 0.5
엔트로피(무질서도)
=>API : DecisionTreeRegressor
=>RandomForest 나 GBM, XGBoost , LightGBM의 기반이 되는 모델
=>다양한 파라미터가 존재하기 때문에 하이퍼 파라미터 튜닝이 필수
=>스케일링 과정은 필요 없음 ->시각화 graphiz 작
#API 사용
m = 200
X = np.random.rand(m,1)
y = 4 * (X-0.5) ** 2 + np.random.randn(m,1)/10
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg.fit(X,y)
4)SVM(Support Vector Machine)
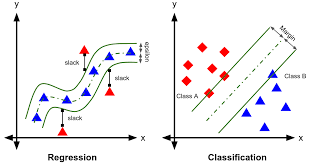
=> 분류에서는 가장 가까운 데이터와의 거리가 가장 먼 결정 경계를 만들어가는 방식
=> 회귀에서는 제한된 마진 오류안에서 가능한 많은 샘플이 들어가도록 학습
마진 오류의 폭은 epsilon 파라미터로 설정
=> API는 sklearn.svm.LinearSVR 이 선형 SVM 회귀이고 비선형은 SVR클래스인데 이 경우는 epsilon외에도 kernel, degree(kernel이 poly일 때 추가할 다항식의 차수), C(규제)와 같은 하이퍼 파라미터를 추가로 사용합니다.
=> 선형 SVM 적용
#데이터 생성
np.random.seed(42)
m = 50
X = 2 * np.random.rand(m, 1)
y = (4 + 3 * X + np.random.randn(m, 1))
X_train = X[:40]
y_train = y[:40]
X_test = X[40:]
y_test = y[40:]
#선형 SVM 생성 및 훈련
from sklearn.svm import LinearSVR
#epsilon 은 결정 경계의 폭 - 이 안에 데이터를 배치
#이 값이 작을 수록 훈련 데이터에 정확해지고 클수록 훈련 데이터와 잘 안맞습니다.
epsilons = [0.1 ,0.5,1.0,1.5,2.0]
for epsilon in epsilons:
svm_reg = LinearSVR(epsilon = epsilon, random_state = 42)
svm_reg.fit(X_train, y_train)
y_pred = svm_reg.predict(X_test)
mse = mean_squared_error(y_test,y_pred)
rmse=np.sqrt(mse)
print(epsilon,":",rmse)
'Study > Machine learning,NLP' 카테고리의 다른 글
| 머신러닝(7)-실습1 (1) | 2024.03.06 |
|---|---|
| 머신러닝(6)-Ensemble (0) | 2024.03.05 |
| 머신러닝(4)-Regression(1) (0) | 2024.03.04 |
| 머신러닝(3)-Classification(2) (0) | 2024.02.29 |
| 머신러닝(2)-Classification(1) (0) | 2024.02.28 |



