1.차원 축소
1)개요
=>머신 러닝의 많은 훈련 샘플들은 여러 개의 특성을 가지고 있음
=>특성의 개수가 많으면 훈련을 느리게 하고 좋은 솔루션을 찾기 어렵게 만드는데 이러 문제를 차원의 저주라고 합니다
=>실전 문제에서는 특성 수를 크게 줄여서 불가능한 문제를 가능한 범위 내로 변경해야 하는 경우가 많습니다
2)차원의 저주
=> 고차원에서는 많은 것이 상당히 다르게 동작
=>사각형 안에서 점을 무작위로 선택하면 경계션에서 0.001 정도 거리에 존재할 확률이 0.4% 정도 되는데 10,000 차원이 되면 경계선에 존재할 확률이 99.99999%보다 커짐
=> 대부분의 훈련 데이터가 서로 멀리 떨어져 있게 되고 새로운 샘플도 멀리 떨어져 있을 가능성이 높아지게 되서 이 경우 예측을 위해서는 훨씬 더 많은 외삽을 수행해야 합니다.
변수의 값을 추정하는 과정 중의 하나가 외삽인데 변수 들 간의 관계를 이용해서 값을 추정하는 것
보간법은 하나의 속성에서 값과 값 사이의 데이터를 추정하는 것이고 외삽은 여러 변수 사이에서 값을 추정
3)차원 축소의 종류
=>feature selection
-개요
특성 선택은 특정 피처에 종속성이 강한 불필요한 피처는 제거하고 데이터의 특성을 잘 나타내는 주요 피처만 선택하는 것
통계적인 방법을 이용해서 feature들의 중요도에 순위를 정해 결정하는 방법
정보 손실이 발생
동일한 문제를 해결하는 다른 데이터 세트에서는 중요도의 순위가 달라질수 있으
-구현 방법
필터 방식
전처리 단계에서 통계 기법을 사용해서 변수를 채택하는 방법
높은 상관계수의 feature를 선택
변수 중요도나 상관도에 관련된 알고리즘
상관 계수
불순도(트리 모델에서 사용하는 지니계수 나 엔트로피)
카이 제곱 검정
래퍼 방식
예측 정확도 측면에서 가장 좋은 성능을 보이는 피처 집합을 뽑아내는 방법
변수 선택 평가 모델
AIC(Akaike Information Criteria)
BIC(Bayesian Information Criteria)
수정 R2 (결정 계수)
여러번 머신러닝 알고리즘을 수행해야 되기 떄문에 비용이 높게 발생하지만 가장 좋은 피처의 집합을 찾는 원리이기 때문에 모델의 정확도를 위해서는 바람직한 방법
알고리즘
-Foward Selection(전진 선택법):피처가 없는 상태에서 부터 반복할 떄마다 피처를 추가하면서 성능이 가장 좋아지는 지점을 찾는 방식
-Backward Selection(후진 선택법):전체 feature을 가지고 덜 중요한 피처를 제거하면서 성능의 향상이 없을 때까지 수행하는 방식
-Stepwise Selection(단계별 선택법): 피처가 없는 상태에서 출발해서 전진 선택법과 후진 소거법을 번갈아가면서 수행하는 방식인데 가장 시간이 오래 걸리는 방식이지만 가장 우수한 예측성능을 나타내는 변수 집합을 찾아낼 가능성이 높음
임베디드 방식
Filtering 과 Wrapper 의 조합
각각의 피처를 직접 학습하며 모델의 정확도에 기여하는 피처를 선택
계수가 0 이 아닌 피처를 선택해서 더 낮은 복잡성으로 모델을 훈련하는 방식
라쏘, 릿지,엘라스틱 넷 등을 이용해서 규제를 추가할 수 있음
=>피처 추출( feature extraction)
-개요
기존 feature를 저 차원의 중요 feature로 압축해서 추출하는 것
새롭게 만든 feature는 기존의 feature와는 다른 값
새로 만들어지는 피처는 기존 피처를 단순하게 압축하는 것이 아니라 함축적으로 더 잘 설명할 수 있는 다른 공간으로 매 핑해서 추출하는 것
함축적인 특성 추출은 기본 피처가 전혀 인지하기 어려웠던 잠재적인 요소를 추출
이 방식은 전체 피처를 사용
-구현
LinearMethods:PCA,FA,LDA,SVD
NonlinearMethods:KernelPCA,t-SNE,Isomap,Auto-Encoder(생성형 AI의 기반)
4)차원 축소의 목적
=>비용,시간,자원,용량의 문제
-불필요한 변수 저장: 용량 문제가 발생할 수 있음
-차원이 많아지면 비례해서 분석시간이 증가
=>Overfitting 문제
- 변수가 많으면 모델의 복잡도가 증가: 일반화 가능성이 낮음
- 민감도(Sensitivity) 가 증가해서 오차가 커질 수 있는 가능성 높아짐
=>군집화 분석 결과가 좋지 않음
- 벡터간의 거리가 유사해짐
=>차원이 높으면 설명력이 떨어짐
-2~3차원은 시각화가 가능하지만 3차원보다 큰 차원은 시각화가 어렵습니다
-잠재적인 요소를 추출
=>차원을 축소하며 일부 정보가 유실되기 떄문에 훈련속도가 빨라지기는 하지만 성능은 나빠질 가능성이 높습니다.
2.투영(projection)
1)개요
=>물체의 그림자를 어떤 물체 위에 비추는 일 또는 그 비친 그림자를 의미
=>어떤 물체든 그림자는 2차원으로 표현될 수 있다는 원리
=>투영을 이용해서 구현된 알고리즘이 PCA,LDA등
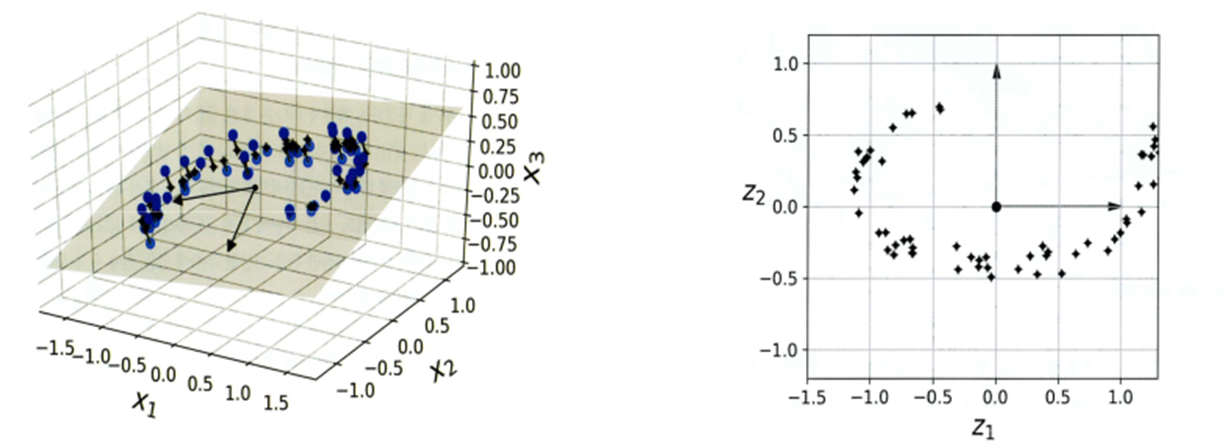
2)특징
=>MNIST 같은 이미지에는 잘 적용이 되지만 스위스 롤같은 데이터에는 적용할 수 없다
=>특성들의 값이 거의 비슷하고 다른 특성의 값이 많이 다르면 적용하기가 좋은데 그렇지 않은 경우는 적용하기가 어렵습니다.
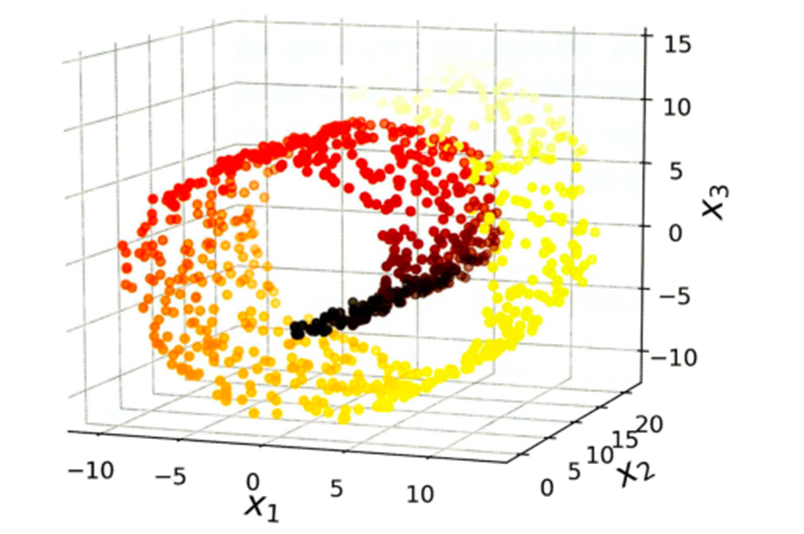
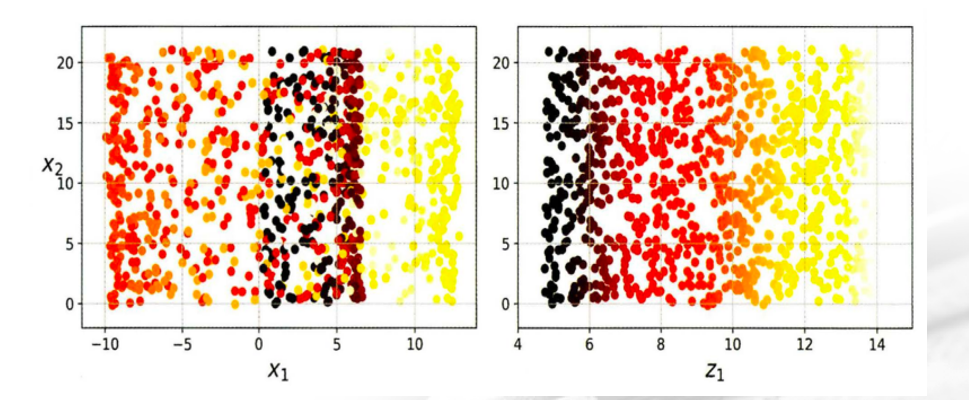
위의 그림에서처럼 된다면 오른쪽 처럼 나오길 바라지만 왼쪽처럼 나와버림
3.Manifold 방식
1)개요
=>차원을 축소하는데 특정차원을 없애지 않고 새로운 차원을 만들어 내는 방식
=>이 방식을 이용하는 알고리즘은 LLE,t-SNE,IsoMap, Auto Encode등

4.PCA(Principal Component Analysis -주성분 분석)
1)개요
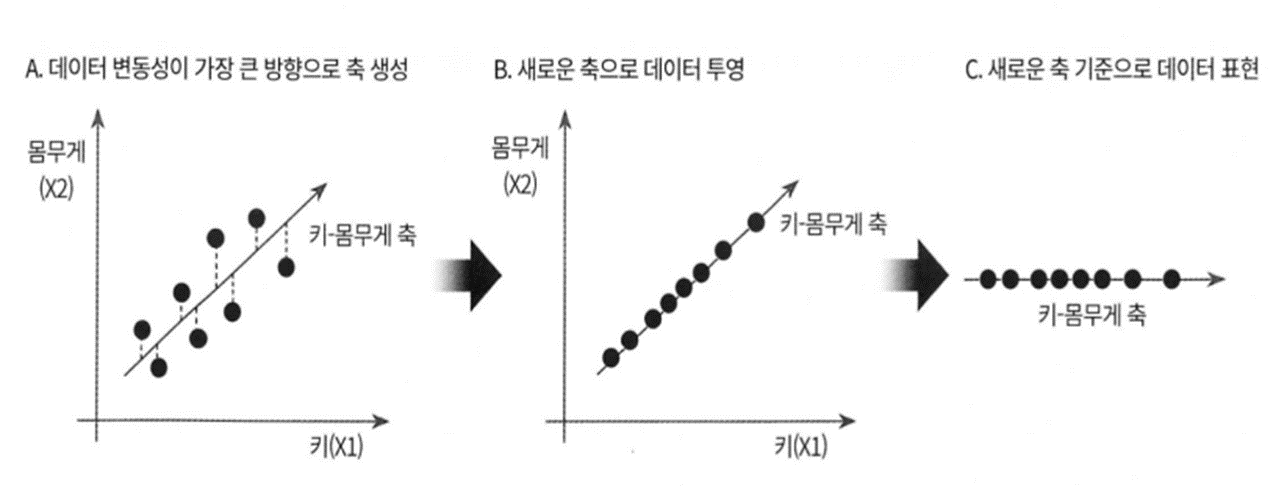
=>여러 변수 간에 존재하는 상관관계를 이용해서 이를 대표하는 주성분을 추출해서 차원을 축소하는 기법
=>차원을 축소할 때 데이터의 정보를 최대한 유지하면서 고차원에서 저차원으로 축소를 하는 방식
=>데이터의 다른 부분을 보존하는 방식으로 분산을 최대한 유지하는 축을 생성
=>이 방식은 데이터의 분포가 표준 정규분포가 아닌 경우에는 적용이 어려움
=> PCA 는 회귀나 분류의 성능을 올리는 목적이 아닌 시각화에 목적을 지님
2)sklearn의 PCA
=>변환기를 데이터 세트에 학습시키고 나면 결과를 확인할 수 있음
=>n_components 라는 매개변수를 축소하고자 차원의 개수를 설정
# 데이터 생성
# feature가 3개인 데이터 생성
np.random.seed(42)
m=60
w1,w2= 0.1, 0.3
noise=0.1
angles = np.random.rand(m)*3*np.pi/3 -0.5
X=np.empty((m,3))
X[:,0]=np.cos(angles) + np.sin(angles)/2 + noise*np.random.randn(m)/2
X[:,1]=np.sin(angles)*0.7 + noise*np.random.randn(m)/2
X[:,2]=X[:,0]*w1 + X[:,1]*w2 + noise + np.random.randn(m)
print(X)from sklearn.decomposition import PCA
#2개의 feature로 주성분 분석을 수행
pca = PCA(n_components=2)
X2D = pca.fit_transform(X)
print(X2D[:5])
=> 분산의 비율
-분산을 얼마나 보존하는 가를 나타내는 지표:Explained Variance Ratio
-각각의 주성분 벡터가 이루는 축에 투영한 결과의 분산의 비율을 의미
-원 데이터 특성을 얼마나 가졌는가를 하는 비율
-일반적으로 70 % 이상의 값을 갖도록 주성분 개수를 설정
-sklearn에서는 PCA 인스턴스의 explained_variance_ratio_ 속성에 배열로 저장
#분산 비율 확인
print(pca.explained_variance_ratio_)
#첫번쨰 주성분이 74%정도 설명 두번쨰 성분은 21%정도도 설명 가능
=>복원
-원래의 차원으로 데이터를 돌리는 것
-PCA 인스턴스의 inverse_transform(주성분분석을 수행한 데이터)
- 복원을 하게 되면 원본 데이터로 복원되지는 않음
why? 분산의 비율이 100프로가 아니기 때문에 일부데이터는 손실
#데이터 복원
X2D_inv = pca.inverse_transform(X2D)
#print(X2D_inv[:5])
#원본 데이터와 복원된 데이터를 비교
print(np.allclose(X2D_inv,X))
#차이의 평균
print(np.mean(np.sum(np.square(X2D_inv-X),axis=1)))
=>적절한 차원 수를 선택
-시각화를 위해서 주성분 분석을 하는 경우은 2~3개로 수행
-시각화 이외의 목적인 경우는 일반적으로 주성분의 개수를 지정하기 보다는 분산의 비율을 이용해서 개수를 설정합니다
n_component 에 성분의 개수가 아닌 0.0~ 1.0 사이의 비율을 설정하면 비율이 되는 주성분의 개수로 분석을 수행
-시각화를 수행해서 엘보가 만들어지는 지점이 있다면 엘보를 이용해서 주성분의 개수를 설정하기도 합니다.
#차원수를 지정해서 PCA 수행: 154 개의 feature 를 찾아서 수행
pca = PCA(n_components=154)
pca.fit_transform(X_train)
#분산의 비율 확인 - 95% 정도 유지됨을 알 수 있음
print(pca.explained_variance_ratio_.sum())
- 아래와 같이 주성분의 비율로 개수를 선언해도 결과가 나옴
#차원수를 지정해서 PCA 수행: 95% 이상 되는 주성분 개수로 주성분 분석
pca = PCA(n_components=0.95)
pca.fit_transform(X_train)
#분산의 비율 확인 - 95% 정도 유지됨을 알 수 있음
print(pca.explained_variance_ratio_.sum())
#차원의 개수 확인
print(pca.n_components_)

- 공통이 많은 부분이 많을수록 PCA 의 효율이 좋다
3)sklearn의 PCA 문제점- Random PCA로 해결
=>모든 데이터를 메모리에 적재시킨 후 훈련을 시켜야 합니다. (공간복잡도가 매우 큼)
=>시간을 많이 소요 (시간복잡도:O(m*n의 제곱) + O(n의 3제곱) )
=>이를 해결하기 위해 Random PCA 등장
=>PCA 에서 svd_solver 매개변수를 randomized 로 지정하면 Random PCA 를 수행하는데 확률적 알고리즘을 이용해서 주성분에 대한 근사값을 찾는 방식
이 방식은 원본 데이터의 차원은 속도에 아무런 영향을 주지 못하고, 주성분의 개수만 훈련 속도에 영향을 줍니다.
=>시간 복잡도가 O(m*d의 제곱) + O(d의 3제곱): d는 줄이고자 하는 차원의 개수,주성분 개수
=>sklearn은 차원의 개수가 500개이상이거나 줄이려는 차원의 개수가 원본 차원의 80%보다 작으면 RandomPCA를 수행
=> Random PCA 는 랜덤으로 축을 하나 만들고 이를 비교해가면서 성능 확인
PCA: 차원개수 + 행의 개수 속도 영향
RandomPCA:주성분개수 + 행의 개수 영향
#차원수를 지정해서 PCA 수행: 95% 이상 되는 주성분 개수로 주성분 분석
pca = PCA(n_components=154,svd_solver ='randomized')
pca.fit_transform(X_train)
#분산의 비율 확인 - 95% 정도 유지됨을 알 수 있음
print(pca.explained_variance_ratio_.sum())
4)점진적 PCA (Incremental PCA)
=>PCA 구현의 문제점 중 하나는 전체 훈련세트를 올려야한다는 것입니다.
=>이를 해결하기 위한 방법중 하나가 IncrementalPCA
=>데이터를 나누어서 학습이 가능: 온라인 학습 이가능
★ ★ ★ ★ ★
Online 학습이 가능: 일부분의 데이터를 가지고 학습한 후 다른 데이터를 추가해서 학습이 가능
Online 학습이 불가능: 전체 데이터를 가지고 학습
=>fit 대신에 partial_fit 이라는 메서드를 이용해서 훈련
=>메모리가 부족한 경우와 실시간으로 데이터가 생성되는 경우 점진적 PCA 를 사용
=>일반 PCA 보다 훈련 시간은 조금 더 걸릴 수 있습니다.
배치 처리가 미니 배치 방식보다 좋은 점은 자원을 효율적으로 사용할 수 있고 작업 시간은 단축 시킬 수 있습니다.
미니 배치 방식이 좋은 점은 훈련을 실시간으로 수행시킬 수 있어 훈련이 끝나는 시점만 따져보면 더 빠릅니다.
=> 파이썬에서 메모리가 정리 되는 방법은 가리키는 데이터가 없을 떄 자동으로 정리가 되고 기존 변수가 가르키는 데이터가 없도록 만드는 방법은 del 변수명을 사용하면 됩니다.
파이썬은 메모리 관리를 reference count라는 방식을 사용합니다.

5)3가지 PCA 방식의 훈련시간 비교
import time
#일반PCA
start_1 = time.time()
pca = PCA(n_components=154,svd_solver='full')
X2D = pca.fit_transform(X_train)
end_1 = time.time()
print("일반PCA수행시간:",end_1-start_1)
print(pca.explained_variance_ratio_.sum())
#RandomPCA
#svd_solver='randomized'를 생략해도 가능 - feature 수가 500개가 넘기때문에
start_2 = time.time()
pca = PCA(n_components=154,svd_solver ='randomized')
X2D = pca.fit_transform(X_train)
end_2 = time.time()
print("RandomPCA수행시간:",end_2-start_2)
print(pca.explained_variance_ratio_.sum())
#IncrementalPCA
from sklearn.decomposition import IncrementalPCA
#배치 사이즈: 데이터를 몇개씩 훈련
n_batches = 100
start_3 = time.time()
inc_pca = IncrementalPCA(n_components=154)
for X_batch in np.array_split(X_train,n_batches):
inc_pca.partial_fit(X_batch)
X_reduced = inc_pca.transform(X_train)
end_3 = time.time()
print("IncrementalPCA수행시간:",end_3-start_3)
print(inc_pca.explained_variance_ratio_.sum())
6)Kernel PCA
=>커널 트릭 PCA: 비선형 데이터에 다항을 추가하는 것처럼 해서 비선형 결정 경계를 만드는 PCA
=>일반 PCA를 수행해서 분산의 비율이 제대로 표현되지 않는 경우 사용
=>KernelPCA 란느 클래스를 사용하고 하이퍼파라미터에 kernel에 linear, rbf,sigmoid 를 설정할 수 있는데 sigmoid는 로그 함수 형태를 의미하고 rbf 는 가우시안 정규 분포 형태의 커널을 적용 gamma 라는 하이퍼 파라미터를 이용해서 복잡도를 설정합니다.
gamma는 0.0~1.0 사이의 값
=>하이퍼 파라미터 튜닝을 거의 하지 않는데 주성분 분석을 분류나 회귀의 전처리 과정을 사용하는 경우에 가장 좋은 성능을 발휘하는 커널이나 gamma 값을 찾기 위해서 하이퍼 파라미터 튜닝을 하는 경우도 있습니다.
from sklearn.decomposition import KernelPCA
pca = PCA(n_components=2)
pca.fit_transform(X)
print(pca.explained_variance_ratio_.sum())
#linear
kernel_pca =KernelPCA(n_components=2,kernel='linear',
fit_inverse_transform=True)
result=kernel_pca.fit_transform(X)
explained_variance = np.var(result,axis=0)
explained_variance_ratio = explained_variance /np.sum(explained_variance)
print(explained_variance_ratio)
#sigmoid
kernel_pca =KernelPCA(n_components=2,kernel='sigmoid',
coef0=1,gamma=0.002,
fit_inverse_transform=True)
result=kernel_pca.fit_transform(X)
explained_variance = np.var(result,axis=0)
explained_variance_ratio = explained_variance /np.sum(explained_variance)
print(explained_variance_ratio)
#rbf
kernel_pca =KernelPCA(n_components=2,kernel='rbf',
fit_inverse_transform=True)
result=kernel_pca.fit_transform(X)
explained_variance = np.var(result,axis=0)
explained_variance_ratio = explained_variance /np.sum(explained_variance)
print(explained_variance_ratio)
=>kernel PCA 사용 목적: 데이터를 설명하고자가 아닌 분류나 회귀 할 때 시간 단축 및 복잡도를 낮추기 위해서 진행
지도학습은 결과에 대한 옳고 그름을 내가 내리는게 아닌 정답이 따로 존재. 비지도 학습은 정답을 분석가가 내리는게 맞음
7)PCA 수행 이유
=>시각화를 하거나 단순한 모델을 만들기 위해서 PCA 을 수행합니다
=>PCA 를 수행해서 분류나 회귀 작업을 수행하게 되면 성능은 떨어질 가능성이 높지만 일반화 가능성은 높아집니다.
실세계에 존재하는 데이터는 잡음이 섞인 경우가 많아서 잡음이 섞인 데이터을 가지고 훈련을 하게 되면 overfitting될 가능성이 높습니다.
8)실습
# 노이즈가 없는 입력 데이터 출력
def plot_digits(data):
fig, axes = plt.subplots(4, 10, figsize=(10, 4),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i, ax in enumerate(axes.flat):
ax.imshow(data[i].reshape(8, 8),
cmap='binary', interpolation='nearest',
clim=(0, 16))
#원본 이미지 출력
plot_digits(digits.data)
#잡음 추가
np.random.seed(42)
noisy = np.random.normal(digits.data, 4)
plot_digits(noisy)
#주성분 분석
from sklearn.decomposition import PCA
#70% 정도 분산을 나타내는데 26개의 feature 필요
pca = PCA(n_components=0.7).fit(noisy)
print(pca.n_components_)
#PCA 를 수행한 데이터를 복원
components = pca.transform(noisy)
filtered = pca.inverse_transform(components)
plot_digits(filtered)
=>아까보다 잡음 부분이 없어짐
5.LLE
=>지역 선형 임베딩 ( Locally Linear Embedding)은 비선형 차원 축소 방법
=>피처 내의 모든 데이터를 이용하지 않고 가장 가까운 이웃에 얼마나 선형적으로 연관되어 있는 측정한 후 국부적인 관계가 가장 잘 보존되는 저차원을 찾는 방식
=>LocallyLinearEmbeding 클래스를 제공하고 n_components 로 차원의 개수를 설정하고 n_neighbors 에 이웃의 개수를 설정합니다.
#스위스 롤은 롤 케익처럼 클래스가 구분된 데이터를 생성
#첫번째 리턴되는 값은 feature 3개로 구성된 feature 의 배역
#두번째 리턴되는 값은 범주에 해당하는 타겟입니다.
X,t = make_swiss_roll(n_samples = 1000,noise = 0.2, random_state=42)
from sklearn.manifold import LocallyLinearEmbedding
#10개의 이웃을 이용해서 2개의 성분 축소
lle = LocallyLinearEmbedding(n_components=2,n_neighbors=10,random_state=42)
X_reduced = lle.fit_transform(X)
plt.scatter(X_reduced[:,0],X_reduced[:,1],c=t,cmap=plt.cm.hot)
plt.show()

위 그림은 LLE , 아래그림은 일반적인 PCA 만 진행했을 텐데 , LLE 같은 경우에는 X축으로 분류가 보임. PCA 도 분류할 수는 있지만 복잡한 식을 계산해야됨.
6.LDA(Linear Discriminant Analysis -선형 판별 분석)
=>분류 알고리즘이지만 훈련 과정에서 개별 클래스를 분별할 수 있는 축을 학습
=>각 클래스 간의 분산과 클래스 내부에서의 분산을 이용
=>클래스 간의 분산은 최대한 크게하고 내부의 분산은 최대한 작게 가져가는 방식
=>LDA 나 LLE을 이용해서 차원을 축소할 때는 스케일링을 해주어야 합니다.
=>sklearn.discriminant_analysis.LinearDiscriminantAnalysis 클래스로 구현되어 있고, 하이퍼파라미터는 n_components
from sklearn.datasets import load_iris
iris =load_iris()
X=iris.data
y=iris.target
#각 feature 간의 거리 차이가 다르기 때문에 스케일링 해줘야함
print("스케일링 이전값")
print(X[:,0].max()-X[:,0].min())
#print(X[:,1].max()-X[:,1].min())
#print(X[:,2].max()-X[:,2].min())
#print(X[:,3].max()-X[:,3].min())
from sklearn.preprocessing import MinMaxScaler
X_scaled = MinMaxScaler().fit_transform(X)
print("스케일링 이후값")
print(X_scaled[:,0].max()-X_scaled[:,0].min())
#print(X_scaled[:,1].max()-X_scaled[:,1].min())
#print(X_scaled[:,2].max()-X_scaled[:,2].min())
#print(X_scaled[:,3].max()-X_scaled[:,3].min())
print("스케일링 이전 평균, 표준편차")
print(X[:,0].mean())
print(X[:,0].std())
print("MINMAX스케일링 이후 평균, 표준편차")
print(X_scaled[:,0].mean())
print(X_scaled[:,0].std())
from sklearn.preprocessing import StandardScaler
X_standardscaled = StandardScaler().fit_transform(X)
print("STANDARD스케일링 이후 평균, 표준편차")
print(X_standardscaled[:,0].mean())
print(X_standardscaled[:,0].std())
7.기타 차원 축소 알고리즘
1)NMF : 행렬 분해를 이용해서 차원을 축소
2)Random Projection:랜덤 투영
3)Multi Dimensional Scaling
=>샘플간의 거리를 유지하면서 차원을 축소
4)Isomap
5)t-SNE
=>비슷한 샘플은 가까이 비슷하지 않은 샘플은 멀리 떨어지도록 하면서 차원을 축소
=> 고차원 공간에 있는 샘플의 군집을 시각화 할 때 사용
=>고도로 군집된 데이터의 경우 가장 잘 작동하지만 속도가 느림
=>일반 PCA 가 많이 사용되었던 이유는 분산을 시반으로 하기 때문에 차원의 개수를 설정하는 것이 쉽고 빠름
PCA 의 단점은 비선형 관계를 보존할 수 없다는 것
고차원의 데이터를 축소할 때는 t-SNE 나 Isomap을 주로 이용
'Study > Machine learning,NLP' 카테고리의 다른 글
| NLP(1)- 자연어 처리 (0) | 2024.03.13 |
|---|---|
| 머신러닝(10)-군집 (0) | 2024.03.11 |
| 머신러닝(8)-실습(2) (0) | 2024.03.07 |
| 머신러닝(7)-실습1 (1) | 2024.03.06 |
| 머신러닝(6)-Ensemble (0) | 2024.03.05 |



