1.Clustering
=>분류는 피처를 가지고 이미 만들어져 있는 레이블에 할당하는 작업이고 레이블이 없어서 피처들을 가지고 그룹을 만드는 작업
=>군집이 이용되는 분야
-고객 분류
-데이터 분석: 데이터를 분석할 떄 전체 데이터를 가지고 분석을 하는 경우도 있지만 군집을 한 후 데이터 분석을 하는 것이 더 효과적인 경우가 많음
-차원 축소
-이상치 탐지
모든 클러스터에 친화성이 낮은 샘플이 존재한다면 이 샘플은 이상치일 가능성이 높음
웹사이트 내 행동을 기납으로 사용자 클러스터를 만든 경우 초 당 웹 서버 요청을 비정상적으로 많이 하는 사용자를 감지 해서 이상치로 판정할 수 있음
-준지도 학습: 일부분만 label 이 존재하는 경우 레이블이 없는 데이터에 레이블을 할당
-검색 엔진
-이미지 분할: 물체 탐지 및 추적 시스템을 이용
=>과일 이미지 군집
-fruits_300.npy :사과, 파인애플, 바나나 3가지 이미지를 각각 100개씩 numpy 배열
-흑백 이미지를 사용할 때 우리 관심 대상은 배경이 아니고 물체이므로 255에서 뺴서 반전된 값을 사용하는 경우가 많습니다
컴퓨터에서는 255 가 흰색이고 0이 검정색이라서 배경이 값을 가지게 되고 실제물체가 0이 되는 일이 발생합니다.
원래 이미지로 반전해서 출력하고자 하면 cmap 에 gray 대신에 gray_r 을 설정하면 됩니다
#모든 이미지 데이터의 차원을 1차원으로 변경
apple = fruits[0:100].reshape(-1,100*100)
pineapple = fruits[100:200].reshape(-1,100*100)
banana = fruits[200:300].reshape(-1,100*100)
#이미지 별 픽셀의 평균을 히스토그램으로 출력
plt.hist(np.mean(apple,axis=1))
plt.hist(np.mean(pineapple,axis=1))
plt.hist(np.mean(banana,axis=1))
plt.legend(['apple','pineapple','banana'])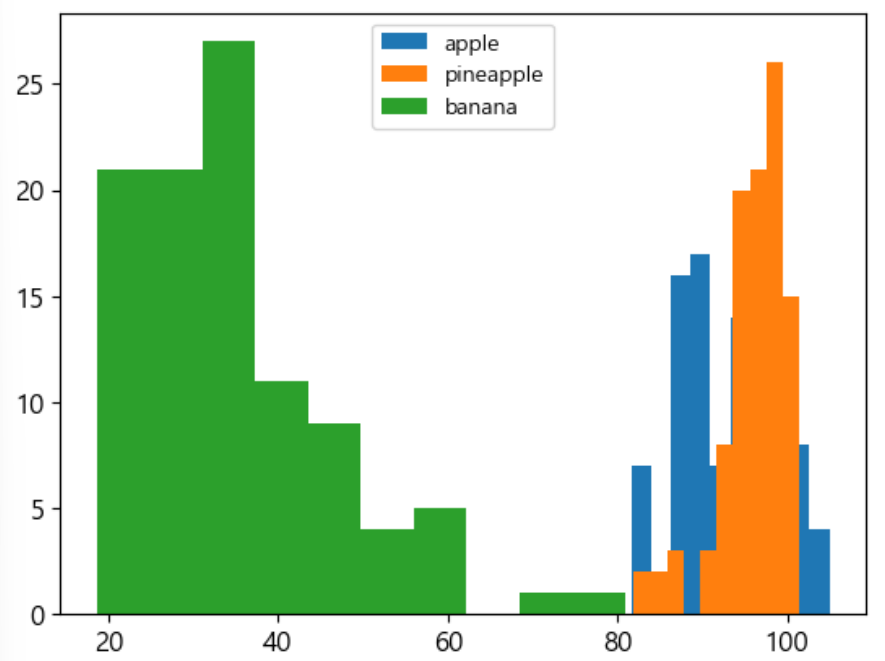
-banana는 길고 얇아서 평균을 내면 apple이나 pineapple 에 비해 평균이 낮음
-apple 과 pineapple 은 평균으로는 크게 차이가 안남
-픽셀 평균 값으로만으로 바나나는 확실히 구분할 수 있음
#각 이미지의 픽셀 단위 값을 히스토그램으로 출력
fig , axs = plt.subplots(1,3,figsize=(20,5))
axs[0].bar(range(10000),np.mean(apple,axis=0))
axs[1].bar(range(10000),np.mean(pineapple,axis=0))
axs[2].bar(range(10000),np.mean(banana,axis=0))
plt.show()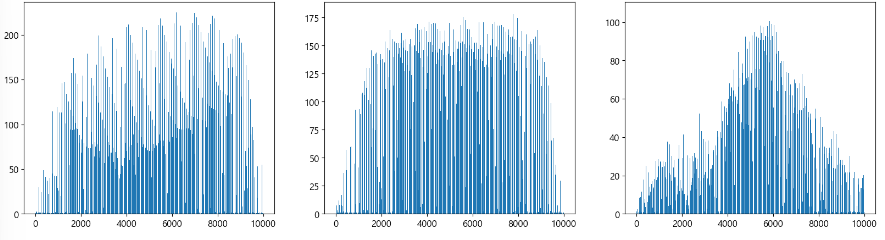
-픽셀 단위로 확인해본 결과 사과와 파인애플의 평균은 차이가 남
2.K-Means 알고리즘
1)개요
=>맨 처음 군집의 개수만큼 랜덤하게 중심점을 설정
=>모든 데이터를 중심점에 가까운 클러스터로 할당
=>중심점을 클러스터의 중앙으로 업데이트
=>다시 데이터들을 중심점에 가까운 클러스터로 배정하게 됨.
=>일정한 횟수 안에서 변경이 발생하지 않으면 종료

2) API
=>sklearn.cluster.KMeans(n_cluster=8,init='k-means++',n_init=10,max_iter=300,tol=1e-5,verbose=0,random_state=None,n_jobs=1)
-n_cluster:군집의 개수
-init:centroid 을 설정하는 방법
-max_iter: centroid 최대 이동 횟수
-verbose :1이면 훈련도중 로그를 출력
=>훈련 후 사용할 수 있는 속성
labels_:군집의 결과
cluster_centers_: centroid 좌표(시각화 용도로 이용)
=>실습
from sklearn.datasets import make_blobs
#중심점 좌표
blob_centers = np.array( [[ 0.2, 2.3],
[-1.5 , 2.3],
[-2.8, 1.8],
[-2.8, 2.8],
[-2.8, 1.3]])
blob_std = np.array([0.4, 0.3, 0.1, 0.1, 0.1])
X, y = make_blobs(n_samples=2000, centers=blob_centers,
cluster_std=blob_std, random_state=7)
#데이터 분포 시각화
def plot_clusters(X, y=None):
plt.scatter(X[:, 0], X[:, 1], c=y, s=1)
plt.xlabel("$x_1$", fontsize=14)
plt.ylabel("$x_2$", fontsize=14, rotation=0)
plt.figure(figsize=(8, 4))
plot_clusters(X)
plt.show()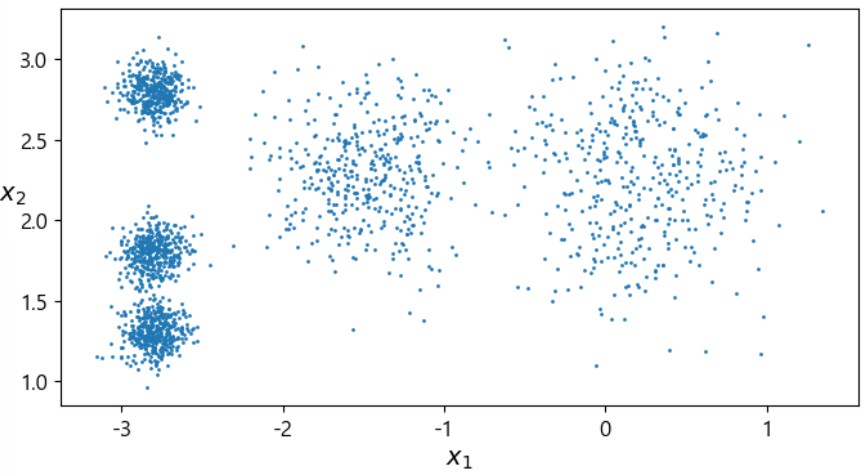
#군집을 수행
from sklearn.cluster import KMeans
#클러스터 개수
k = 5
kmeans = KMeans(n_clusters=k, random_state=42)
y_pred = kmeans.fit_predict(X)
print(y_pred[:100]) #예측한 클러스터
print(y[:100]) #생성할 때 사용한 타겟을 출력
#이둘을 절대 같이 비교해서는 안됨예측값과 실제 값을 서로 비교하면 안되는 이유가 index 번호가 달라져서 나옴
#k-means center 값 찾기
print(kmeans.cluster_centers_)#예측
print(kmeans.predict(np.array([[0,2]])))
3)centroid 초기화
=>centroid 의 위치를 어느 정도 예측할 수 있다면 init 파라미터에 centroid 의 list 를 담은 배열을 설정하고 n_init을 1로 설정하면 됩니다.
=>랜덤 초기화를 사용할 수 있는데 이 경우는 n_init 매개변수에 횟수를 지정하면 되는데 이 경우 한 번의 fit 메서드 호출 때마다 n_init 개수만큼 랜덤하게 초기화를 수행하고 최적의 solution을 반환합니다.
=>최적의 solution 을 선택하는 방법은 각 샘플과 centroid 사이의 평균 제곱 거리를 가지고 평가하는데 이를 inertia(이너셔)라고 합니다.
=>inertia_라는 속성을 이용해서 알 수 있고 score() 메서드를 통해서 inertia 의 음수값을 확인할 수 있습니다.
=>sklearn은 높은 숫자가 좋은 모델이라고 판단을 하기 떄문에 score 는 항상 높은값이 좋다라고 판정을 합니다.
=>k-Means ++ 알고리즘
랜덤하게 centroid 를 선택하는 경우 잘못해서 centroid 사이의 거리가 가까우면 최적이 아닌 솔루션으로 수렴할 가능성이 있습니다.
하나의 centroid 를 설정하고 다음 centroid를 설정할 때 기존 centroid에서 먼 centroid를 설정합니다.
sklearn은 기본적으로 이 방식을 사용하는데 이 방식이 랜덤초기화 보다는 시간이 더 걸리지만 충분한 가치가 있다고 판단을 합니다.
특별한 경우가 아니면 이 방식을 이용합니다.
4)속도 개선
=>k-Means 라는 모든 데이터의 거리를 계산했는데 찰스 엘칸의 논문에서는 centroid 와 거리에 상한과 하한을 두어서 상한 이상이면 더 이상 거리를 계산하지 않고 centroid를 재선정하는 방식
=>elkan의 논문
-centroid 로 부터의 거리 계산을 할 떄 상한과 하한을 만들어서 상한이나 하한을 벗어나면 더이상 거리 계산 수행하지 않고 다음 작업으로 진행하는 방식
-sklearn에서는 기본으로 설정되어 있고 이를 사용하지 않으려면 algorithm 매개변수를 full로 설정해야 합니다.
=>Mini-Batch기법
-centroid 을 옮겨서 거리 계산을 할 때 전체 데이터의 거리를 계산하지 않고 일부분의 데이터만 거리 계산을 수행하는 방법
-MiniBatchKMeans 라는 클래스를 이용
#전체 거리 계산을 수행하는 KMEANS
import time
k=5
start_time =time.time()
kmeans = KMeans(n_clusters=k,random_state=42,algorithm='full')
y_pred = kmeans.fit_predict(X)
end_time = time.time()
print("전체거리 계산 수행 시간:",end_time-start_time)
#군집의 성능 평가 기준 중 하나로 centroid 와 의 거리 제곱합의 제곱근
print(kmeans.inertia_)
#거리의 상한과 하한을 이용해서 군집을 수행하는 K-Means
k=5
start_time =time.time()
kmeans = KMeans(n_clusters=k,random_state=42,algorithm='elkan')
y_pred = kmeans.fit_predict(X)
end_time = time.time()
print("엘칸 거리 계산 수행 시간:",end_time-start_time)
#군집의 성능 평가 기준 중 하나로 centroid 와 의 거리 제곱합의 제곱근
print(kmeans.inertia_)
#mini-batch 군집을 수행하는 K-Means
from sklearn.cluster import MiniBatchKMeans
k=5
start_time =time.time()
kmeans =MiniBatchKMeans(n_clusters=k,random_state=42)
y_pred = kmeans.fit_predict(X)
end_time = time.time()
print("mini-batch 계산 수행 시간:",end_time-start_time)
#군집의 성능 평가 기준 중 하나로 centroid 와 의 거리 제곱합의 제곱근
print(kmeans.inertia_)

- 일반적인 K-Means >> mini-batch >> 엘칸 거리 를 순으로 시간이 걸립니다.
- inertia_(이너셔) 는 mini-batch > K-Means == 엘칸 거리의 결과가 나왔습니다.
5)적절한 클러스터 개수의 선택
=>inertia을 이용하는 방법
- inertia는 centroid 와의 거리이므로 이값이 작은 것
-inertia 는 centroid 와의 거리이므로 이 값이 작은 것을 선호한다고 했으므로 이 값이 작은 모델을 선택하는데 클러스터의 개수가 많아질수록 inertia 의 값은 작아질 가능성이 높습니다.
무한정 클러스터의 개수를 늘릴 수는 없기 떄문에 일반적으로 클러스터 개수별로 이너셔의 값을 시각화 한후 elbow( 변화량이 급격하게 줄어드는 지점) 가 발생하는 지점을 선택하는 것을 권장합니다.
kmeans_k = [KMeans(n_clusters=k,random_state=42,algorithm='elkan').fit(X) for k in range(1,10)]
inertias = [model.inertia_ for model in kmeans_k]
print(inertias)
plt.plot(range(1,10), inertias)
plt.show()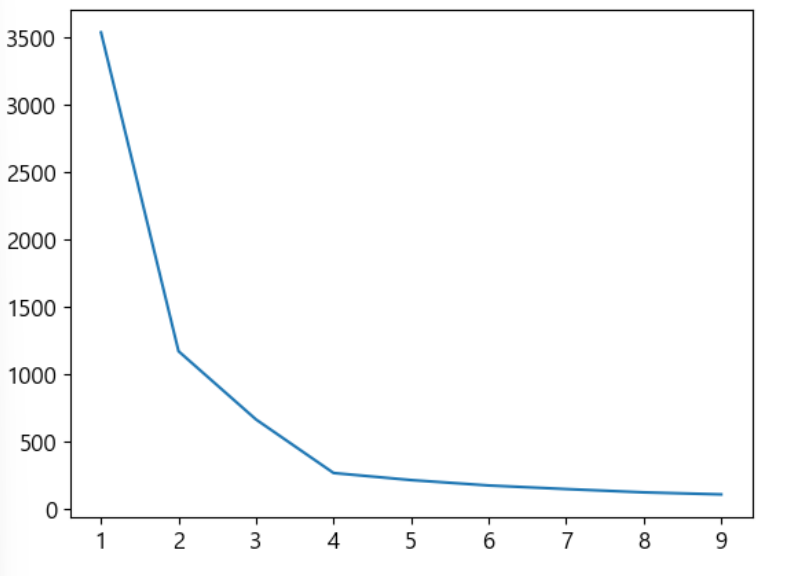
-시각화를 통해서 inertia 를 선택할 수 있습니다.
-inertia 값이 cluster 가 4개일 때 까지는 급격하게 줄어들지만 5 이후 부터는 완만하게 줄어듭니다. 이 경우에는 4개의 클러스터를 선택하는 것이 효율적인 군집
=>실루엣 계수를 이용하는 방법
- 실루엣 계수: (b-a)/ max(a,b)
b는 가장 가까운 클러스터 까지의 평균 거리
a는 동일한 클러스터 내에서 다른 샘플까지의 평균 거리
이 값은 -1 부터 1까지 나올 수 있는데 +1 이면 자신의 클러스터 내에서는 거리가 가깝고 다른 클러스터의 샘플까지의 거 리는 먼 경우이며 0에 가까운 값이면 클러스터 경계에 샘플이 많이 분포된 경우이고 -1 에 가까우면 군집이 잘못된 것으 로 간주합니다.
-API
sklearn.metrics.silhouette_sample(X,labels,metric = 'euclidean'): X는 feature가 되고 , labels는 군집의 결과를 대입하면 모든 데이터의 실루엣 계수를 계산해서 리턴
sklearn.metrics.silhouette_score(X,labels,metric = 'euclidean'): 실루엣 계수의 평균을 리턴해주는데 일반적으로 이 값이 크면 군집이 잘 되었다고 판단할 수 있지만 무조건은 아님
전체 평균값이 크면 좋기는 하지만 개별 군집과의 차이도 고려를 해야 합니다
kmeans_k = [KMeans(n_clusters=k,random_state=42,algorithm='elkan').fit(X) for k in range(1,20)]
silhouette_scores = [silhouette_score(X,model.labels_)for model in kmeans_k[1:]]
print(silhouette_scores)
plt.plot(range(2,20), silhouette_scores)
plt.show()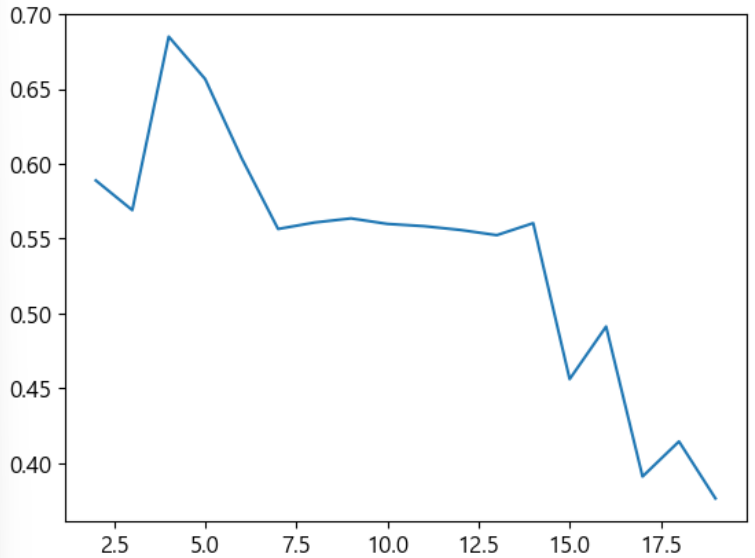
6)한계
=>알고리즘이 쉽고 간결하면 속도가 빠르고 확장이 용이하다는 장점을 가짐
=>최적의 솔루션을 만들려면 알고리즘을 여러 번 수행해야 함
=>클러스터의 개수를 직접 설정해야 함
=>거리 기반 알고리즘이라서 속성의 개수가 많은 경우 군집화 정도가 떨어지게 되므로 PCA 를 수행한 후 적용해야 할 수도 있음
=>클러스터의 크기나 밀집도가 서로 다른 경우 잘 작동하지 않음
from sklearn.datasets import make_moons
#0 과 1 두가지 클래스를 가진 반원 모양의 데이터 생성
X,y = make_moons(200,noise=0.05,random_state=42)
plt.scatter(X[:,0],X[:,1],s=50,cmap='viridis')
print(y)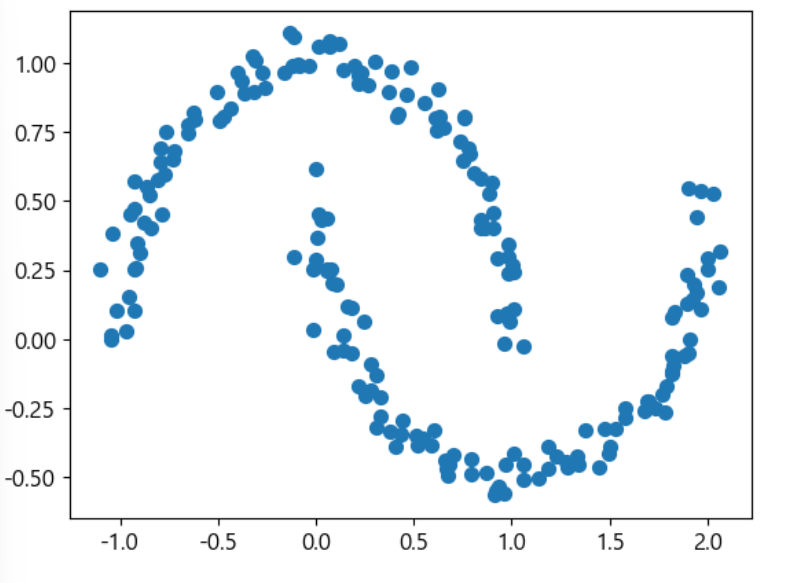
위 데이터를 KMeans하면 반원끼리 연결하고 싶지만 아래와 같은 결과가 나온다
labels =KMeans(2,random_state=42).fit_predict(X)
plt.scatter(X[:,0],X[:,1],c=labels,s=50,cmap='viridis')
print(y)
7) 군집 활용
=>Image Segmentation
-이미지를 여러개로 분할하는 것
-이 작업은 현재는 CNN(합성곱 신경망) 으로 대부분 수행
-항공 사진을 이용해서 삼림이나 논을 구분해 내는 것이 군집을 이용한 이미지 분할의 대표적인 활용이었습니다
-딥러닝이 아직까지는 속도의 영향
from matplotlib.image import imread
#533 * 800 의 컬러 이미지
image =imread(".\google.png")
#이미지 출력 - 머신러닝이나 딥러닝에서는 이미지를 1차원으로 만들어 사용하는 경우가 있음
#출력 할 때는 가로 * 세로 * 색상 차원 변경해서 사
plt.imshow(image)
print(image.shape)
# 이미지의 차원으로 변경
#3차원 이미지를 2차원으로 수정
X= image.reshape(-1,3)
kmeans = KMeans (n_clusters=8,random_state=42).fit(X)
#군집한 결과 가져오기
#레이블 된 데이터의 중심점의 값을 가져오기 - 8개로 압축된 결과
segmented_img = kmeans.cluster_centers_[kmeans.labels_]
plt.imshow(segmented_img.reshape(image.shape))
plt.show()
segmented_imgs =[]
n_colors = (20,10,8,6,4,2)
for n_clusters in n_colors:
kmeans = KMeans(n_clusters=n_clusters,random_state=42).fit(X)
segmented_img = kmeans.cluster_centers_[kmeans.labels_]
segmented_imgs.append(segmented_img.reshape(image.shape))
for idx,segmented_img in enumerate(segmented_imgs):
plt.subplot(232+idx-1)
plt.imshow(segmented_img)
plt.title(n_colors[idx])
plt.show()

컬러 이미지를 몇 개의 클러스터로 군집을 하는 것은 차원 축소의 효과도 가져올 수 있습니다.
차원 축소를 수행하면 일반화 효과가 더 높아질 수 있습니다.
이미지 데이터의 경우 군집을 수행한 후 분류를 해보면 검증 했을 때 점수가 더 높게 나오기도 합니다.
=>군집을 수행한 후의 이미지 분류 ★
#분류 모델 훈련 및 결과 확인
from sklearn.linear_model import LogisticRegression
log_reg =LogisticRegression(multi_class='ovr',solver='lbfgs',
max_iter=5000,random_state=42)
log_reg.fit(X_train,y_train)
log_reg_score = log_reg.score (X_test,y_test)
print(log_reg_score)
from sklearn.pipeline import Pipeline
from sklearn.cluster import KMeans
pipeline = Pipeline([
('kmeans',KMeans(n_clusters=50,random_state=42)),
('log_reg',LogisticRegression(multi_class='ovr',solver='lbfgs',
max_iter=5000,random_state=42))
])
pipeline.fit(X_train,y_train)
print(pipeline.score(X_test,y_test))일반적으로 군집한 결과를 피처로 추가하고 학습을 하면 예측 성능이 우수해 질 가능성이 있습니다.
GridSearchCV 등을 이용해서 최적의 하이퍼파라미터를 찾아서 수행해보면 됩니다.
=>준지도학습
- 레이블이 없는 데이터가 많고 레이블이 있는 데이터가 적을 떄 사용
-레이블이 없는 데이터에 레이블을 추가하기 위해서 사용
-대표 이미지를 생성: 각 클러스터에서 centroid 에 가장 가까운 이미지
-대표 이미지를 이용해서 레이블을 생성한 후 전파
#이전에 사용한 숫자 이미지 데이터에서 훈련 데이터 중 50개만 라벨링이 된 경우
#이 데이터를 가지고 분류 모델을 만들게 되면 정확도가 많이 떨어짐
n_labeled = 50
log_reg = LogisticRegression(multi_class='ovr',solver='lbfgs',
random_state=42,max_iter=5000)
log_reg.fit(X_train[:n_labeled],y_train[:n_labeled])
print(log_reg.score(X_test,y_test))
#0.83333
#대표 이미지 생성을 위한 군집을 수행
kmeans = KMeans(n_clusters=50,random_state=42)
X_digits_dist = kmeans.fit_transform(X_train)
#print(X_digits_dist)
#centroid 와의 거리가 가장 가까운 샘플 데이터 찾기
representative_digit_idx = np.argmin(X_digits_dist,axis=0)
print(representative_digit_idx)
X_representative_digits = X_train[representative_digit_idx]
#임의의 레이블을 생성 - 대표 이미지의 현재 레이블 값
y_train[representative_digit_idx]
#각 대표 이미지에 할당할 레이블
y_representative_digits = np.array([4, 8, 0, 6, 8, 3, 7, 7, 9, 2, 5, 5, 8, 5, 2, 1, 2, 9, 6, 1, 1, 6,
9, 0, 8, 3, 0, 7, 4, 1, 6, 5, 2, 4, 1, 8, 6, 3, 9, 2, 4, 2, 9, 4,
7, 6, 2, 3, 1, 1 ])
n_labeled = 50
log_reg = LogisticRegression(multi_class='ovr',solver='lbfgs',
random_state=42,max_iter=5000)
#군집을 수행해서 생성된 대표 이미지와 레이블을 이용해서 학습
log_reg.fit(X_representative_digits,y_representative_digits)
print(log_reg.score(X_test,y_test))
#0.92222
#레이블 전파 : 대표 이미지에 라벨링한 값을 라벨이 없는 데이터들에 대입
#훈련 데이터에 레이블을 만들기 위해서 훈련 데이터 만큼의 빈 배열을 생성
y_train_propagated = np.empty(len(X_train),dtype=np.int32)
for i in range(50):
y_train_propagated[kmeans.labels_==i] = y_representative_digits[i]
log_reg = LogisticRegression(multi_class='ovr',solver='lbfgs',
random_state=42,max_iter=5000)
log_reg.fit(X_train,y_train_propagated)
print(log_reg.score(X_test,y_test))
데이터를 수집할 떄 라벨링이 되어있지 않다고 데이터를 사용하지 않거나 하는 것은 바람직하지 않습니다
라벨링 되지 않는 데이터에 군집을 이용해서 라벨링을 하고 분류를 수행하면 라벨링된 데이터만 가지고 분류를 수행하는 것보다 효과적인 경우가 종종 있습니다
실세계의 모든 데이터가 라벨링 된 경우는 거의 없고 대부분은 일부 라베링 데이터를 가지고 지금처럼 유추해야하는 경우가 많습니다.
3.계층적 클러스터링(Hierarchical Clustering)
1)개요
=>계층적인 트리로 클러스터를 조직하는 방법
=>특이점 또는 비정상적인 그룹이나 레코드 발견하는데 민감
=>직관적인 시각화가 가능(화이트 박스)
=>용어
-Dendrogram: 계층적 클러스터를 시각적으로 표현
-Distance
-Dissimilarity(비유사도)
=>데이터가 수십만개가 넘어가는 경우에는 사용하기가 어려움
트리 기반은 컴퓨터의 리소스를 많이 필요로 합니다.
데이터의 크기가 작은 문제에 주로 사용
=>방법
분할 계층 군집: 전체 데이터를 포함하는 하나의 클러스터에서 시작해서 더 작은 클러스터로 반복적으로 나누는 방식인 클러스터 안에 데이터가 1개 남을 때까지 계속
병합 계층 군집:각 샘플이 독립적인 클러스터가 되고 하나의 클러스터가 남을 때까지 가장 가까운 클러스터를 합쳐 나가는 방식
2) 병합 계층 군집
=>상향식(bottom -up) 으로 클러스터 묶기
=>묶는 방법: 클러스터의 개수를 설정하지 않음
-단일 연결(single linkage): 합칠때 가장 비슷한 샘플 간 거리를 계산해서 거리가 가까운 클러스터를 묶는 방식
-완전 연결(complete linkage): 가장 비슷하지 않은 샘플을 비교해서 병합을 수행
=>알고리즘
-평균 연결(average linkage): 평균을 가지고 거리를 계산
-중심 연결: 중앙값을 가지고 거리를 계산
-와드 연결(ward linkage): 분산을 이용해서 클러스터링 ->표편차가 적을수록 좋음
=>거리 계산
-샘플 데이터 생성
np.random.seed(42)
#feature
variables = ['X','Y','Z']
#행의 이름(인덱스) - 5개
labels = ['ID_0','ID_1','ID_2','ID_3','ID_4']
X = np.random.random_sample([5,3])*10
df = pd.DataFrame(X, columns=variables, index=labels)
df
#거리 계산 - 유클리디안 거리
from scipy.spatial.distance import pdist, squareform
row_dist = pd.DataFrame(squareform(pdist(df, metric='euclidean')),
columns=labels,
index=labels)
row_dist
=>scipy.clustering.hierarchy 모듈에 계층적 클러스터링을 위한 API 제공
-pdist 에 축약된 거리 행렬이나 ndarray를 설정하는데 ndarray 를 설정하면 metric 으로 거리를 계산할 방법을 작성해야 합니다.
-method 에 연결 방식 설정
#계층적 클러스터링 수행
from scipy.cluster.hierarchy import linkage
#완전 연결 방식을 이용한 상향식 클러스터링 수행
row_clusters = linkage(row_dist, method='complete')
pd.DataFrame(row_clusters,
columns=['row label 1', 'row label 2','distance','no. of items in clust.'],
index=['cluster %d' %(i+1) for i in range(row_clusters.shape[0])])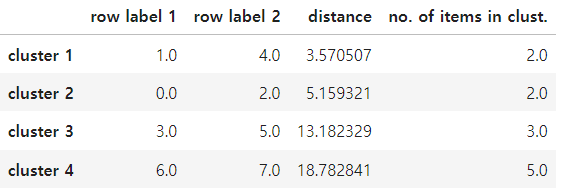
첫번쨰와 두번쨰는 묶인 트리의 클러스터 이름이고 세번쨰는 클러스터간의 거리이고 네번쨰는 클러스터 안의개수
이 경우는 처음 시작할 때 5개의 데이터이므로 클러스터이름 0 -4 묶일때마다 클러스터가 번호가 순차적으로 추가됩니다.
=>scipy.cluster.hierarchy.dendrogram 을 이용해서 시각화 가능
#계층형 클러스터링 시각화
from scipy.cluster.hierarchy import dendrogram
row_dendr = dendrogram(row_clusters,labels=labels)
plt.tight_layout()
plt.ylabel('유클리디안 거리')
plt.show()
=>sklearn에서도 AgglomerativeClustering 클래스를 이용해서 상향식 계층 군집이 가능
- 하이퍼 파라미터도 군집의 개수(n_clusters)를 설정해야함
n_clusters:군집의 개수
affinity:거리 계산 방법
linkage:알고리즘(ward,average,complete)
4.평균 이동 (Mean Shift)

1)수행 방식
=>각 샘플을 중심으로 하는 원을 그리고 그 다음 원마다 안에 포함된 샘플의 평균을 구함
=>원의 중심을 평균점으로 이동
=>모든 원이 움직이지 않을 떄 까지 이 평균이동을 계속 수행
=>최대 밀도를 찾을 떄 까지 높은 쪽으로 원을 이동시키는 방식
4.GMM(Gaussian Mixture Model)
1)개요
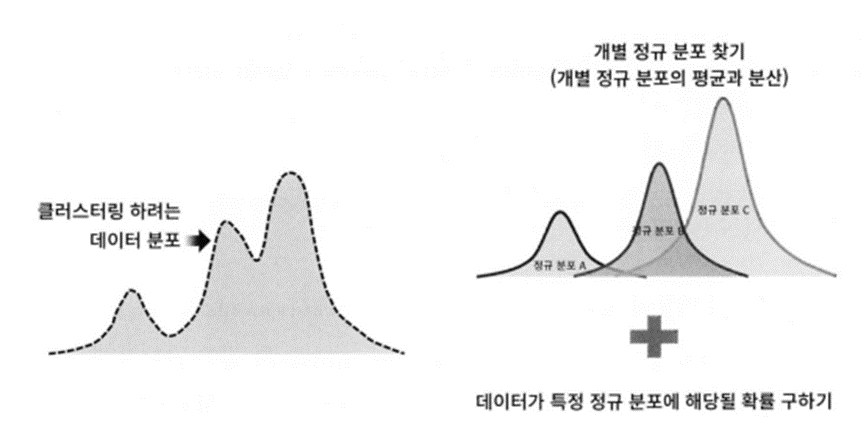
=>데이터는 샘플이 파라미터가 알려지지 않은 여러 개의 혼합된 Gaussian 분포에서 생성되었다고 가정하는 확률 모델
=>하나의 Gaussian 분포에서 생성된 모든 샘플은 하나의 클러스터를 형성한다고 가정
일반적으로 클러스터는 타원형
=>정규 분포(Normal Distribution)
- 평균을 중심으로 데이터는 분포되고 좌우 표준편차 1사이에 전체 데이터의 68.27% 그리고 좌우 표준편차 2에 전체 데이터의 95.45% 를 자니는 분포
- 평균이 0 이고 표준편차가 1인 표준정규분포
- 정규 분포를 가우시안 분포라고도 함
=>데이터 세트가 주어지면 이를 구성하는 여러 개의 정규 분포 곡선을 추출하고 개별 데이터가 어떤 정규 분포에 속하는지 결정하는 방식
=>sklearn.mixture.GaussianMixture API 를 이용해서 군집을 수행
파라미터는 n_components 와 n_init 이 있습니다.
=>예측(predict - 하드 군집)이 가능하고 확률(predict_proba- 소프트 군집) 도 계산
X1, y1 = make_blobs(n_samples=1000, centers=((4, -4), (0, 0)), random_state=42)
X1 = X1.dot(np.array([[0.374, 0.95], [0.732, 0.598]]))
X2, y2 = make_blobs(n_samples=250, centers=1, random_state=42)
X2 = X2 + [6, -8]
X = np.r_[X1, X2]
y = np.r_[y1, y2]
from sklearn.mixture import GaussianMixture
gm = GaussianMixture(n_components=3, n_init=10, random_state=42)
gm.fit(X)
2)제약
=>GMM 모델을 사용하다 보면 특성이나 클러스터가 많거나 샘플이 적을 떄는 최적의 솔루션으로 수렴하기 어려운데 이 떄 클러스터의 모양과 방향의 범위를 제한할 수 있습니다.
=>covariance_type 하이퍼파라미터에 설정
-spherical:모든 클러스터가 타원형으로 만들어지지만 지름은 다를 수 있음
-diag:클러스터는 크기에 상관없이 어떤 타원형도 가능하지만 타원의 축은 좌표 축과 나란해야함
-tied:모든 클러스터가 동일한 타원 모양, 크기 ,방향을 가져야함
-full: 기본값으로 모양, 크기,방향에 대한 제약이 없음
3)클러스터 개수
=>KMeans 는 inertia 나 실루엣 점수를 이용해서 클러스터 개수 선택
실루엣 점수가 높은 것이 좋은 모델이지만 실루엣 점수를 각 군집의 실루엣 점수를 비교를 행햐 조금 더 좋은 모델을 만들 수 있습니다.
=>GMM은 inertia 나 실루엣 점수를 사용할 수 없음
근본적으로 inertia 나 실루엣 점수는 거리의 개념을 갖기 때문에 타원형이나 크기가 많이 다르면 적용하기 어려움
=>GMM에서는 2개의 평가 지표를 사용
-BIC(Bayesian Information Criterion): 샘플의 개수와 학습할 파라미터의 개수를 고려
-AIC(Akaike Information Criterion): 샘플의 개수만 고려
-bic 와 aic 라는 메서드를 이용해서 제공하고 낮은 것이 좋은 모델
-2개의 값이 반대되는 경향을 갖는 경우는 BIC 에 우선권을 둠
#클러스터 개수를 1개부터 10개까지 갖는 GMM 모델을 생성
gms_per_k = [GaussianMixture(n_components=k,n_init=10,random_state=42).fit(X)
for k in range(1,11)]
#bic 와 aic 값을 전부 저장
bics =[model.bic(X) for model in gms_per_k]
aics =[model.aic(X) for model in gms_per_k]
plt.plot(range(1,11),bics,'bo-',label='BIC')
plt.plot(range(1,11),aics,'go--',label='AIC')
plt.show()
#2개의 값 모두 3까지는 줄어들다 4부터 높아집니다
#3개의 클러스터로 군집을 만드는 것이 좋습니다
-BayesianGaussianMixture 클래스는 GMM처럼 클러스터링을 수행하는 것은 같은데 각 클러스터에 가중치를 부여해서 중요하지 않은 클러스터에는 가중치를 0을 설정
이 API 를 이용하면 직접 클러스터의 개수를 설정하지 않아도 최적의 클러스터 개수를 알 수 있습니다.
#BayeianGaussianMixture 모델 사용
from sklearn.mixture import BayesianGaussianMixture
bgm = BayesianGaussianMixture(n_components=10,n_init=10,random_state=42).fit(X)
print(np.round(bgm.weights_,3))
4)문제점
=>밀도 추정을 이용하기는 하지만 밀도 추정의 모양이 타원형이어야 하고, 타원형의 모양이 변하게 되면 제대로 감지하지 못합니다
=>반달 모양의 2개의 데이터 세트를에 대해서 군집을 수행해보면 여러 개의 클러스터로 분할 하려고 합니다
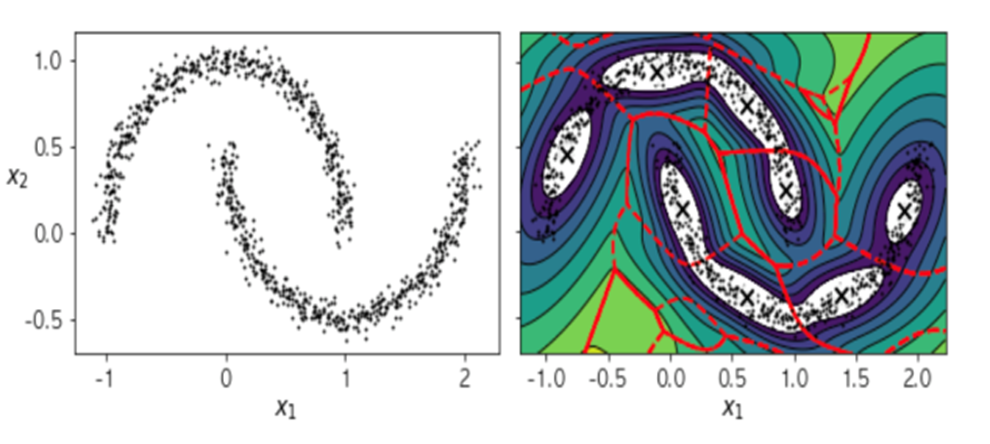
GMM 으로 하다보면 여러 조각으로 분할 시켜버림
=>밀도를 추정하는 모양이 정규 분포에 가까운 타원형만 감지를 해내는 것이 문제
데이터의 분포가 이어지지만 방향이 변경되는 경우 동일한 타원으로 만들어내지 못함
X_moons,y_moons = make_moons(n_samples=1000,
noise=0.05, random_state=42)
bgm = BayesianGaussianMixture(n_components=10,n_init=10,random_state=42).fit(X_moons)
print(np.round(bgm.weights_,2))
타원형 데이터는 잘 구분하는데 반달 처럼 이어지기는 하지만 중간중간 방향이나 기울기가 변경되면 다른 클러스터로 간주 이번의 경우는 8개의 클러스터로 구분했습니다.
5.DBSCAN(Density Based Spatial Clustering of Applications with Noise)
1) 개요
=>국부적인 밀집도를 추정하는 방식으로 임의의 모양을 가진 클러스터를 식별할 수 있는 방식
=>DBSCAM은 특정 공간 내에서 데이터 밀도 차이를 기반 알고리즘으로 하고 있어서 복잡한 기하학적 분포도를 가진 데이터 세트에 대해서도 군집화를 잘 수행

=>일정 영역 안에 일정한 개수의 데이터가 계속 분포한다면 하나의 클러스터로 간주
=>epsilon: 주변 영역
=>min points :최소 데이터 개수
=>데이터를 종류별로 분할
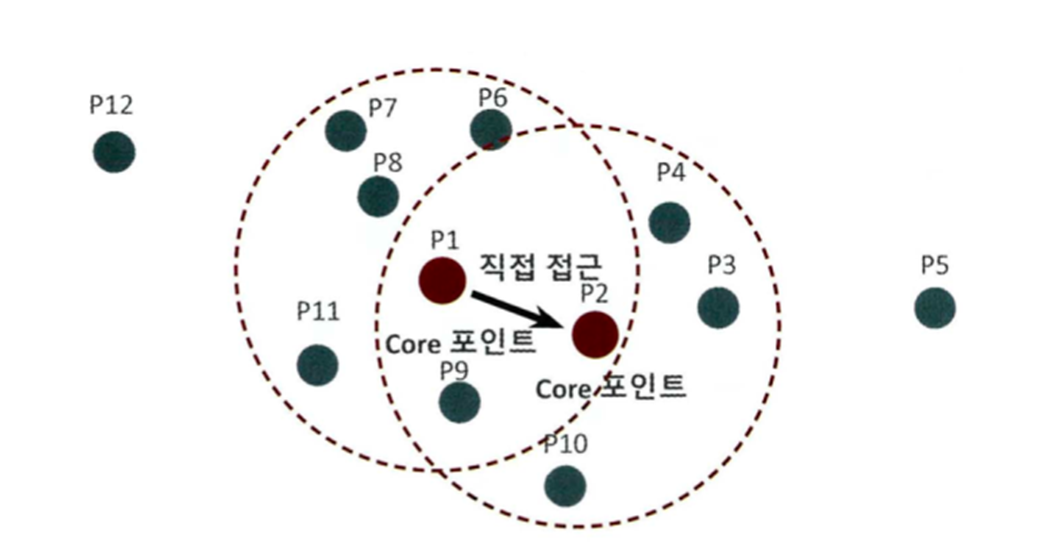
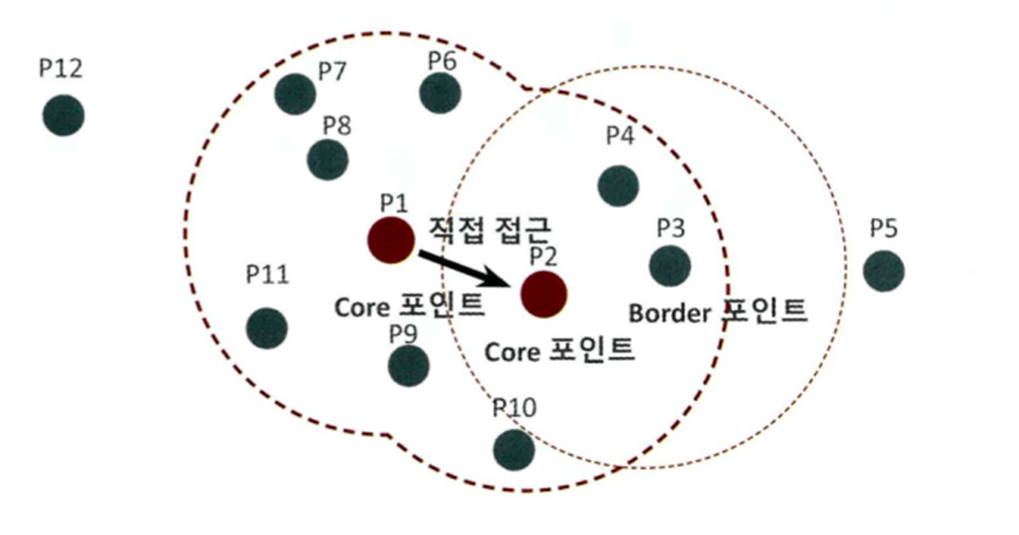
Core point: 자신의 주변 영역 내에 min points 이상의 데이터를 소유한 데이터
Border point:자신의 주변 영역 내에 min points 만큼의 데이터를 가지지는 않지만 Core point 를 이웃으로 가진 데이터
Noise point:자신의 주변 영역 내에 min points 만큼 데이터를 가지지 못하고 Core Point 도 이웃으로 가지지 않는 데이터
=>Core point 와 Border Point를 하나의 클러스터로 묶고 Noise point 는 이상치로 판단
2) 동작 원리
1번

2번

3번

4번

6번
7번

★K-Means vs GMM vs DBSCAN을 각각 언제 쓸까? ★
PCA 를 왜 할까? => 차원 축소 및 시각화 => 일단 2~3개를 축소하고 시각화하고 어떤걸 사용할지 해보기
군집을 해야한다? => 시각화 하고 어떤걸 할껀지 판단해야함 그떄 가장 중요하게 봐야할것이 분포
평균만 보지말고 분산 및 표준편차를 봐야한다
3)중요한 파라미터
eps: 입실론 값으로 주변 영역의 크기를 의미, 이 값이 크면 클러스터링되는 크기가 커지고 작아지면 이상치의 개수가 늘어날 가능성이 높습니다.
-min_samples:주변 영역에 포함되어야 하는 샘플의 최소 개수
from sklearn.datasets import make_moons
from sklearn.cluster import DBSCAN
#반원 모양의 데이터 생성
X,y = make_moons(n_samples=1000,noise=0.05,random_state=42)
#n_components 가 필요없음. 오로지 epsilon과 min_samples 를 활용함
dbscan = DBSCAN(eps = 0.05, min_samples = 5)
dbscan.fit(X)
plt.plot(X[:,0],X[:,1],'k.')
plt.show()
#군집한 결과는 transform으로 return 받아도 되고 , labels_ 속성으로 확인
print(dbscan.labels_)
print(set(dbscan.labels_))
-1 은 Noise Point 로 이상치 판단 - 주위에 샘플이 많지 않음
#core point의 인덱스를 확인
print(dbscan.core_sample_indices_)
=> predict 메서드는 제공하지 않고 fit 과 transform만 제공
predict는 예측을 하는 것인데 예측은 다른 알고리즘이 더 잘 수행하기 때문입니다.
레이블이 없는 경우 DBSCAN 을 이용해서 레이블을 만들고 만들어진 레이블을 이용해서 다른 알고리즘이 분류를 수행합니다.
'Study > Machine learning,NLP' 카테고리의 다른 글
| NLP(2) - 실습 (0) | 2024.03.14 |
|---|---|
| NLP(1)- 자연어 처리 (0) | 2024.03.13 |
| 머신 러닝(9)-차원 축소 (0) | 2024.03.07 |
| 머신러닝(8)-실습(2) (0) | 2024.03.07 |
| 머신러닝(7)-실습1 (1) | 2024.03.06 |



